练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．要用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”，首先应假设两个锐角都大于45°．

    分析 反证法的步骤中，第一步是假设结论不成立，反面成立，可据此进行解答．

    解答 解：“在直角三角形中，至少有一个锐角不大于45°”时应第一步先假设所求证的结论不成立，即为：两个锐角都大于45°．
    故答案是：两个锐角都大于45°．

    点评 本题结合角的比较考查反证法，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

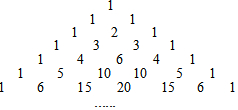    5．杨辉是我国南宋时期杰出的数学家和教育家，如图是杨辉在公元1261年著作《详解九章算法》里面的一张图，即“杨辉三角”，该图中有很多规律，请仔细观察，解答下列问题：
    （1）图中给出了七行数字，根据构成规律，第8行中从左边数第3个数是21；
    （2）利用不完全归纳法探索出第n行中的所有数字之和为2n-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，点D、E、F分别是BC、AD、BC的中点，若△ABC的面积是20，则△BEF的面积为5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．用平面去截一个立方体，截面不可能是（　　）
    A．正方形B．五边形C．六边形D．七边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知某水库的警戒水位为18.8m，值班人员记录了某一周内的水位变化情况，如下表：（单位：m，上周末刚好到达警戒水位，取警戒水位为0，“+”表示水位比前一天升高，“-”表示水位比前一天降低）
    星期一二三四五六日
    变化情况（m）+0.3+0.4-0.2+0.3+0.4-0.1-0.5
    （1）本周内哪一天水位最高？哪一天水位最低？它们与警戒水位相差多少？
    （2）若超过警戒水位1.5m时就应该开闸放水，以确保大坝安全，本周水库需开闸放水吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB，若BE=4，则AE的长为（　　）
    A．1B．1.5C．2D．2.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

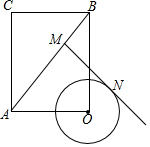    7．如图，在矩形AOBC中，AO=3，BO=4，⊙O的半径为1，点M是矩形对角线AB边上的动点，过点M做⊙O的一条切线MN，切点为N，则切线长MN的最小值是$\frac{\sqrt{119}}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，AB∥CD，点E在线段BC上，若∠1=40°，∠2=30°，则∠3的度数是70°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如果一个多边形的每一个内角都是120°，那么这个多边形是六边形．

    查看答案和解析>>

    同步练习册答案