
分析 (1)用喜欢篮球的人数除以喜欢篮球的人数所占的百分比,即可求出这些被调查的学生数;
(2)用总人数减去喜欢篮球、乒乓球和踢毽子的人数,即可求出喜欢跳绳的人数,从而补全统计图;
(3)根据题意列出表格,得出所有等可能的情况数,找出满足题意的情况数,即可求出所求的概率.
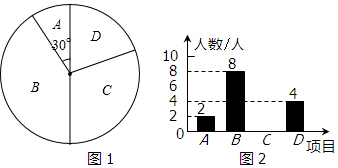
解答 解:(1)由扇形统计图可知:扇形A的圆心角是36°,
所以喜欢A项目的人数占被调查人数的百分比=$\frac{36}{360}$×100%=10%.
由条形图可知:喜欢A类项目的人数有2人,
所以被调查的学生共有2÷10%=20(人),
故答案为:20.
(2)喜欢C项目的人数=20-(2+8+4)=6(人),
因此在条形图中补画高度为6的长方条,如图所示.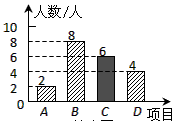
(3)列表如下:
| 甲 | 乙 | 丙 | 丁 | |
| 甲 | --- | (乙,甲) | (丙,甲) | (丁,甲) |
| 乙 | (甲,乙) | --- | (丙,乙) | (丁,乙) |
| 丙 | (甲,丙) | (乙,丙) | --- | (丁,丙) |
| 丁 | (甲,丁) | (乙,丁) | (丙,丁) | --- |
点评 此题考查了条形统计图,扇形统计图,以及列表法与树状图法,弄清题意是解本题的关键.


科目:初中数学 来源: 题型:解答题
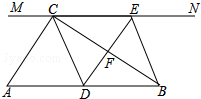 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
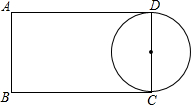 如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE=3.
如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com