
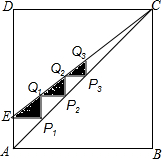
 如图.正方形ABCD的边长为4,点E为AD边上一点.,AE=1,连接AC,CE,过点E作AB的平行线交AC于点P1,过点P1作AD的平行线交CE于Q1,再过Q1作AB的平行线交AC于P2,…如此不断进行下去形成△AEP1,△P1Q1P2,△P2Q2P3,…,记它们的面积之和为S1,类似地形成△EP1Q1,△Q1P2Q2,△Q2P3Q3,…,记它们的面积之和为S2,则$\frac{{S}_{2}}{{S}_{1}}$的值为( )
如图.正方形ABCD的边长为4,点E为AD边上一点.,AE=1,连接AC,CE,过点E作AB的平行线交AC于点P1,过点P1作AD的平行线交CE于Q1,再过Q1作AB的平行线交AC于P2,…如此不断进行下去形成△AEP1,△P1Q1P2,△P2Q2P3,…,记它们的面积之和为S1,类似地形成△EP1Q1,△Q1P2Q2,△Q2P3Q3,…,记它们的面积之和为S2,则$\frac{{S}_{2}}{{S}_{1}}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
分析 先证明${S}_{△E{P}_{1}{Q}_{1}}$:${S}_{△AE{P}_{1}}$=3:4,同理:${S}_{△{Q}_{1}{Q}_{2}{P}_{2}}$:${S}_{△{P}_{1}{P}_{2}{Q}_{1}}$=3:4,…由此即可解决问题.
解答 解:正方形ABCD中,∠CAD=45°,
∵P1Q1∥P2Q2=P3Q3…,
∴∠Q1PC=∠Q2P2C=Q3P3C=…=45°.
∵P1E∥P2Q1∥P3Q2∥…∥AB,
∴△AP1E,△P1Q1P2,△P2Q2P3都是等腰直角三角形,
∴P1E=AE,P1Q1=P2Q1,P3Q2=P2Q2,…
∵CD∥EP1,
∴∠DCE=∠Q1EP1,
∴tan∠DCE=tan∠Q1EP1,=$\frac{DE}{CD}$=$\frac{3}{4}$,
∴$\frac{{P}_{1}{Q}_{1}}{E{P}_{1}}$=$\frac{3}{4}$,
∴${S}_{△E{P}_{1}{Q}_{1}}$:${S}_{△AE{P}_{1}}$=$\frac{1}{2}$•EP1•P1Q1:$\frac{1}{2}$•AE•EP1=3:4,
同理:${S}_{△{Q}_{1}{Q}_{2}{P}_{2}}$:${S}_{△{P}_{1}{P}_{2}{Q}_{1}}$=3:4,…
∴$\frac{{S}_{2}}{{S}_{1}}$=$\frac{3}{4}$.
故选B.
点评 本题考查正方形的性质、等腰直角三角形的性质等知识,解题的关键是探究规律,利用规律解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 67.67×104 | B. | 6.767×1013 | C. | 6.767×105 | D. | 6.767×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
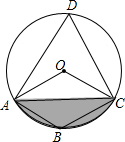 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )| A. | 4$π-3\sqrt{3}$ | B. | 4π$-6\sqrt{3}$ | C. | $\frac{π}{3}$-$\frac{\sqrt{3}}{4}$ | D. | 2$π-3\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.4×105 | B. | 4.4×104 | C. | 44×104 | D. | 0.44×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com