
 点A在反比例函数y=$\frac{3}{x}$的图象上,过点A作AH⊥x轴于点H,连结OA,tan∠AOH=$\frac{1}{3}$.
点A在反比例函数y=$\frac{3}{x}$的图象上,过点A作AH⊥x轴于点H,连结OA,tan∠AOH=$\frac{1}{3}$.分析 (1)设A(3m,m),根据反比例函数图象经过点A可得,3m•m=3,据此可得点A的坐标;
(2)分两种情况进行讨论:①作点H关于AO的对称点B,连接AB,OB,②作点O关于AH的对称点E,分别根据直线AB、AE与双曲线的交点的位置,判段点P的坐标.
解答 解:(1)∵tan∠AOH=$\frac{1}{3}$,
∴$\frac{AH}{OH}$=$\frac{1}{3}$,
∴OH=3AH,
∴设A(3m,m),则3m•m=3,
∴m=1,
∴A(3,1),
故答案为(3,1);
(2)分两种情况:
①如图所示,作点H关于AO的对称点B,连接AB,OB,则
AB=AH=1,BO=HO=3,∠ABO=∠AHO=90°,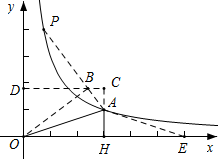
过B作x轴的平行线,交HA的延长线于C,交y轴于D,
设AC=a,则CH=1+a=DO,
由△ABC∽△BOD可得,DB=3a,
∵Rt△BOD中,BD2+OD2=BO2,即(3a)2+(1+a)2=32,
∴a=$\frac{4}{5}$,a=-1(舍去),
∴DB=$\frac{12}{5}$,DO=$\frac{9}{5}$,即B($\frac{12}{5}$,$\frac{9}{5}$),
又∵A(3,1),
∴直线AB的解析式为y=-$\frac{4}{3}$x+5,
解方程组$\left\{\begin{array}{l}{y=-\frac{4}{3}x+5}\\{y=\frac{3}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=\frac{3}{4}}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴直线AB与双曲线交于($\frac{3}{4}$,4)和(3,1)两点;
②如图所示,作点O关于AH的对称点E,则E(6,0),
又∵A(3,1),
∴直线AE的解析式为y=-$\frac{1}{3}$x+2,
解方程组$\left\{\begin{array}{l}{y=-\frac{1}{3}x+2}\\{y=\frac{3}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴直线AE与双曲线交于(3,1)一点,
综上所述,点P的坐标为($\frac{3}{4}$,4).
故答案为:($\frac{3}{4}$,4).
点评 本题主要考查了反比例函数图象上点的坐标特征,反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
 如图一场暴雨后,垂直于地面的一棵树在距地面5米的C处折断,树尖B恰好碰到地面,经测量AB=12米,则原树高为( )
如图一场暴雨后,垂直于地面的一棵树在距地面5米的C处折断,树尖B恰好碰到地面,经测量AB=12米,则原树高为( )| A. | 22米 | B. | 18米 | C. | 17米 | D. | 13米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
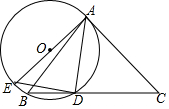 如图,△ABC中,AB=AC,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线交BD的延长线于点C,连接DE.
如图,△ABC中,AB=AC,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线交BD的延长线于点C,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
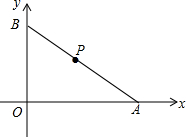 如图,在平面直角坐标系中,点A的坐标是(8,0),点B的坐标是(0,6),点P为线段AB的中点.
如图,在平面直角坐标系中,点A的坐标是(8,0),点B的坐标是(0,6),点P为线段AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
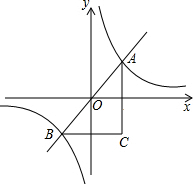 如图,反比例函数y=$\frac{2}{x}$的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于4个面积单位.
如图,反比例函数y=$\frac{2}{x}$的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于4个面积单位.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
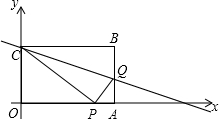 如图,在平面直角坐标系中,矩形OABC的直角边OA、OC分别在x轴的正半轴和y轴的正半轴上,过点C的直线y=-$\frac{1}{3}$x+a交矩形的AB边于点Q,AQ=b.
如图,在平面直角坐标系中,矩形OABC的直角边OA、OC分别在x轴的正半轴和y轴的正半轴上,过点C的直线y=-$\frac{1}{3}$x+a交矩形的AB边于点Q,AQ=b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com