
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
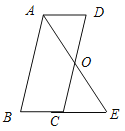
【答案】(1)证明见解析(2)当∠B=∠AEB=45°时,四边形ACED是正方形
【解析】试题分析:(1)根据平行线的性质可得∠D=∠OCE,∠DAO=∠E,再根据中点定义可得DO=CO,然后可利用AAS证明△AOD≌△EOC;
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,首先证明四边形ACED是平行四边形,再证对角线互相垂直且相等可得四边形ACED是正方形.
试题解析:证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠OCE,∠DAO=∠E.∵O是CD的中点,∴OC=OD.在△ADO和△ECO中,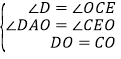 ,∴△AOD≌△EOC(AAS);
,∴△AOD≌△EOC(AAS);
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.
∵△AOD≌△EOC,∴OA=OE.
又∵OC=OD,∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠COE=∠BAE=90°,∴ACED是菱形.∵AB=AE,AB=CD,∴AE=CD,∴菱形ACED是正方形.
故答案为:45.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在横线上填写理由,完成下面的证明. 如图,已知∠1+∠2=180°,∠B=∠3,求证∠C=∠AED
证明:∵∠1+∠2=180°(已知),∠1+∠DFE=180°()
∴∠2=∠DFE()
∴AB∥EF()
∴∠3=∠ADE()
又∵∠B=∠3(已知)
∴∠B=∠ADE()
∴DE∥BC()
∴∠C=∠AED()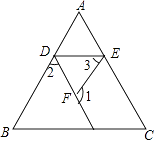
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是 ![]() 的中点,过点D作DE⊥AC,交AC的延长线于点E.
的中点,过点D作DE⊥AC,交AC的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为 . 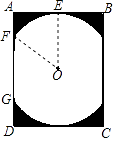
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在平时的练习中,遇到下面一道题目:
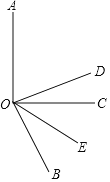
如图,∠AOC=90°,OE 平分∠BOC,OD平分∠AOB.
①若∠BOC=60°,求∠DOE 度数;
②若∠BOC=α(0<α<90°),其他条件不变,求∠DOE 的度数.
(1)下面是某同学对①问的部分解答过程,请你补充完整.
∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ,
∵OD 平分∠AOB,
∴ ,(角平分线的定义)
∴∠DOE= .
(注:符号∵表示因为,用符号∴表示所以).
(2)仿照①的解答过程,完成第②小题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
(1)在同一平面内,不相交的两条直线一定平行.(2)在同一平面内,不相交的两条线段一定平行.(3)相等的角是对顶角.(4)两条直线被第三条直线所截,同位角相等.(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.其中,正确说法的个数是( )
A. 1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
(1)求∠B的度数;
(2)如果AC=3cm,CD=![]() cm,求△ABD的面积.
cm,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为地铁调价后的计价表.调价后小明、小伟从家到学校乘地铁分别需要4元和3元.由于刷卡坐地铁有优惠,因此,他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校的里程多5 km,且小明每千米享受的优惠金额是小伟的2倍,求小明和小伟从家到学校乘地铁的里程分别是多少千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是一张放在平面直角坐标系中的长方形纸片,
是一张放在平面直角坐标系中的长方形纸片,![]() 为原点,点
为原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() .在
.在![]() 边上取一点
边上取一点![]() ,将纸片沿
,将纸片沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
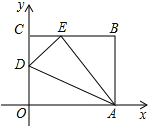
(1)求![]() 和
和![]() 的长;
的长;
(2)求直线![]() 的表达式;
的表达式;
(3)直线![]() 与
与![]() 平行,当它与矩形
平行,当它与矩形![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com