
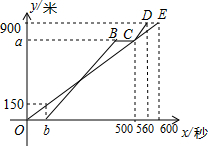
 甲、乙两人从学校出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.
甲、乙两人从学校出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.分析 (1)终点E的纵坐标就是路程,横坐标就是时间;
(2)首先求得C点对应的横坐标,即a的值,则CD段的路程可以求得,时间是560-500=60秒,则乙跑步的速度即可求得;
B点时,所用的时间可以求得,然后求得路程是150米时,甲用的时间,就是乙出发的时刻,两者的差就是所求;
解答 解:(1)根据图象可以得到:甲共跑了900米,用了600秒,则速度是:900÷600=1.5米/秒;
(2)甲跑500秒时的路程是:500×1.5=750米,∴a=750,b=150÷1.5=100,
(3)甲跑500秒时的路程是:500×1.5=750米,则CD段的长是900-750=150米,时间是:560-500=60秒,则速度是:150÷60=2.5米/秒;
甲跑150米用的时间是:150÷1.5=100秒,则甲比乙早出发100秒.
乙跑750米用的时间是:750÷2.5=300秒,则乙在途中等候甲用的时间是:500-300-100=100秒,
故答案为:900,1.5,750,100,2.5,100.
点评 本题考查了识别函数图象的能力,是一道较为简单的题,观察图象提供的信息是关键.


科目:初中数学 来源: 题型:选择题
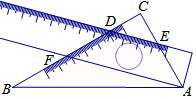 一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相 交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为( )
一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相 交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.
已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com