
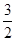 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.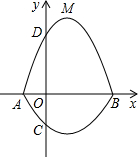
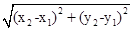 .
.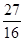 ;(3)-1或-
;(3)-1或-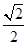 .
.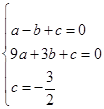 ,解得
,解得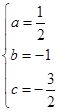 ,
,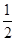 x2-x-
x2-x-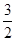 .
.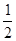 n2-n-
n2-n-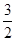 )(0<n<3)
)(0<n<3)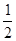 ×
×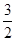 ×n+
×n+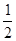 ×3×(-
×3×(-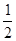 n2+n+
n2+n+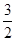 )-
)-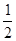 ×3×
×3×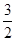
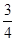 (n-
(n-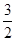 )2+
)2+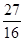
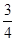 <0,
<0,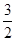 时S∆PBC的最大值是
时S∆PBC的最大值是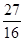
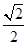 (m=
(m=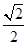 舍去).
舍去).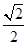 时,△BDM为直角三角形.
时,△BDM为直角三角形.

科目:初中数学 来源:不详 题型:解答题
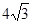 时,求x的值.
时,求x的值.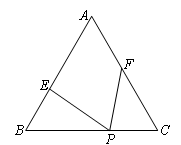
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
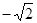 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.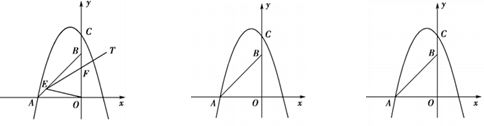
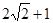 )倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
)倍.若存在,请直接写出点P坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
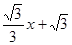 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点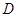 是劣弧AO上一动点(
是劣弧AO上一动点(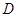 点与
点与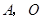 不重合).抛物线y=-
不重合).抛物线y=-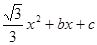 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,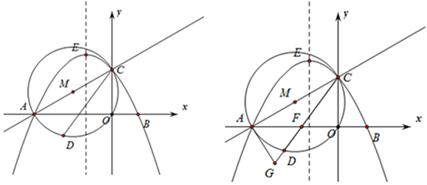
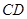 交
交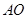 于点
于点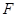 ,延长
,延长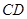 至
至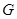 ,使
,使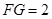 ,试探究当点
,试探究当点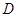 运动到何处时,直线
运动到何处时,直线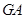 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
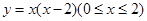 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .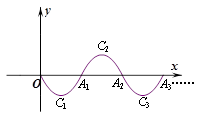
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
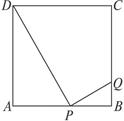
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com