
 如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.
如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出. 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:选择题
| A. | (y+$\frac{7}{4}$)2=$\frac{25}{16}$ | B. | (y-$\frac{7}{4}$)2=$\frac{25}{16}$ | C. | (y+$\frac{7}{2}$)2=$\frac{25}{16}$ | D. | (y-$\frac{7}{2}$)2=$\frac{25}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
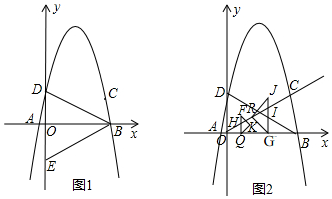
 抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.
抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$=±$\sqrt{5}$ | B. | (-$\sqrt{0.36}$)2=-0.36 | C. | $\root{3}{64}$=4 | D. | $\sqrt{(-3)^{2}}$=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com