练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．下面表格列出了函数y=ax2+bx+c（a，b、c是常数，且a≠0），部分x与y对应值，那么方程ax2+bx+c=0的一个根x的取值范围是（　　）
     x 6.17 6.18 6.19 6.20
     y-0.03-0.01 0.02 0.04
    A．6＜x＜6.7B．6.7＜x＜6.18C．6.18＜x＜6.19D．6.9＜x＜9.20

    分析 根据二次函数的增减性，可得答案．

    解答 解：由表格中的数据，得
    在6.17＜x＜6.20范围内，y随x的增大而减小，
    当x=6.18时，y=-0.01，当x=6.19时，y=0.02，
    方程ax2+bx+c=0的一个根x的取值范围是6.18＜x＜6.19，
    故选：C．

    点评 本题考查了图象法求一元二次方程的近似解，解答此题的关键是利用函数的增减性．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．解下列方程组
    （1）$\left\{\begin{array}{l}{4x-y=1}\\{y=2x+3}\end{array}\right.$             
    （2）$\left\{\begin{array}{l}{5x+y=2}\\{x-3y=4}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

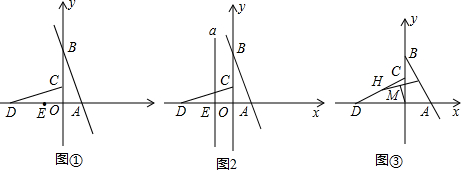
    17．四个村庄A、B、C、D位置如图，现要在平面内建造一个天然气供应站，并从供应站向四个村庄铺设天然气管道，为使铺设的管道总长最短，则天然气供应站应建造的位置是（　　）
    A．点A处B．线段AC的中点处
    C．任意两村庄所连线段的中点处D．线段AC和线段BD的交点处

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知x=$\sqrt{3}$+$\sqrt{2}$，y=$\sqrt{3}$-$\sqrt{2}$，求代数式x2+y2-xy-2x+2y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图①，直线l：y=mx+n（m＜0，n＞0）与x，y轴分别相交于A，B 两点，将△AOB绕点O逆时针旋转90°，得到△COD，
    （1）若l：y=-3x+3，E为AD的中点
    ①在CD上有一动点F，求当△DEF与△COD相似时点F的坐标；
    ②如图②，过E作x轴的垂线a，在直线a上是否存在一点Q，使∠CQO=∠CDO？若存在，求出Q点坐标；若不存在，请说明理由
    （2）如图③，若l：y=mx-4m，G为AB中点，H为CD中点，连接GH，M为GH中点，连接OM．若OM=$\sqrt{10}$，直接写出l的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，EF∥AD，∠1=∠2，试判断DG与AB的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，一次函数，一次函数y=kx+5（k为常数，k≠0）的图象与反比例函数$y=\frac{8}{x}$的图象相交于A（2，b），B两点．
    （1）求一次函数的表达式；
    （2）若将直线AB向下平移m（m＞0）个单位长度后与反比例函数的图象只有一个公共交点，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，AB∥CD，直线EF与AB，CD相截，若∠5=62°，则∠4的度数是（　　）
    A．28°B．62°C．118°D．146°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知点P坐标为（0，2），点A是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的一个动点，直线AP与抛物线的另一个交点为点B，连结AO，BO．
    （1）当点A的纵坐标为5时，求点B的坐标；
    （2）判断以点A为圆心，AP为半径的圆与x轴的位置关系，并说明理由；
    （3）求证：∠AOP=∠BOP．

    查看答案和解析>>

    同步练习册答案