
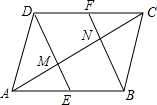
 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点.分析 (1)根据平行四边形的性质:平行四边的对边相等,可得AB∥CD,AB=CD;根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据平行四边的性质:平行四边形的对边相等,可得AB∥CD,AB=CD,∠CDM=∠CFN;根据全等三角形的判定,可得答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵E、F分别是AB、CD的中点,
∴BE=DF,
∵BE∥DF,
∴四边形EBFD为平行四边形;
(2)证明:∵四边形EBFD为平行四边形,
∴DE∥BF,
∴∠CDM=∠CFN.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAC=∠DCA,∠ABN=∠CFN,
∴∠ABN=∠CDM,
在△ABN与△CDM中,
$\left\{\begin{array}{l}{∠BAN=∠DCM}\\{AB=CD}\\{∠ABN=∠CDM}\end{array}\right.$,
∴△ABN≌△CDM (ASA).
点评 本题考查了平行四边形的判定与性质,利用了平行四边形的判定与性质,全等三角形的判定,根据条件选择适当的判定方法是解题关键.


科目:初中数学 来源: 题型:填空题
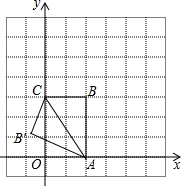 如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).
如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有800人.
某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有800人.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于$\frac{9\sqrt{5}}{2}$.
已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于$\frac{9\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
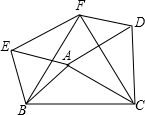 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com