
 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1. 分析 如图,连接AM,由题意得:CA=CM,∠ACM=60°,得到△ACM为等边三角形根据AB=BC,CM=AM,得出BM垂直平分AC,于是求出BO=$\frac{1}{2}$AC=1,OM=CM•sin60°=$\sqrt{3}$,最终得到答案BM=BO+OM=1+$\sqrt{3}$.
解答 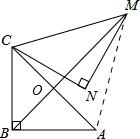 解:如图,连接AM,
解:如图,连接AM,
由题意得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CM,∠MAC=∠MCA=∠AMC=60°;
∵∠ABC=90°,AB=BC=$\sqrt{2}$,
∴AC=2=CM=2,
∵AB=BC,CM=AM,
∴BM垂直平分AC,
∴BO=$\frac{1}{2}$AC=1,OM=CM•sin60°=$\sqrt{3}$,
∴BM=BO+OM=1+$\sqrt{3}$,
故答案为:1+$\sqrt{3}$.
点评 本题考查了图形的变换-旋转,等腰直角三角形的性质,等边三角形的判定和性质,线段的垂直平分线的性质,准确把握旋转的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
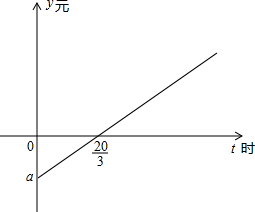 某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.
某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-2 | B. | a+2 | C. | $\frac{a-2}{a-3}$ | D. | $\frac{a-3}{a-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com