
| A. | ∠A+∠C=∠B | B. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,b=$\frac{1}{5}$ | C. | (b+a)(b-a)=c2 | D. | ∠A:∠B:∠C=5:3:2 |
分析 根据三角形内角和定理可分析出A、D的正误;根据勾股定理逆定理可分析出C、B的正误.
解答 解:A、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC为直角三角形,故此选项不合题意;
B、∵$\frac{1}{3}$2+$\frac{1}{4}$2≠$\frac{1}{5}$2,
∴不能构成直角三角形,故此选项符合题意;
C、∵(b+a)(b-a)=c2
c2=b2-a2,
∴a2+c2=b2,
∴△ABC为直角三角形,故此选项不合题意;
D、设∠A=5x°,∠B=3x°,∠C=2x°,
5x+2x+3x=180,
解得:x=18,
则5x°=90°,
是直角三角形,故此选项不合题意;
故选:B.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


科目:初中数学 来源: 题型:选择题
| A. | -33与(-3)3 | B. | $\frac{{2}^{3}}{3}$与($\frac{2}{3}$)3 | C. | -|-2|与-(-2) | D. | -12与(-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
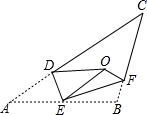 如图,△ABC中,点E是AB中点,点D、F分别在AC、BC上,将△AED、△BEF分别沿ED、EF翻折,使顶点A、B都落在点O处,若∠CDO+∠CFO=98°,则∠C的度数( )
如图,△ABC中,点E是AB中点,点D、F分别在AC、BC上,将△AED、△BEF分别沿ED、EF翻折,使顶点A、B都落在点O处,若∠CDO+∠CFO=98°,则∠C的度数( )| A. | 40° | B. | 41° | C. | 42° | D. | 43° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )| A. | SSS | B. | SAS | C. | SSA | D. | ASA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com