
【题目】如图所示,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.
秒.
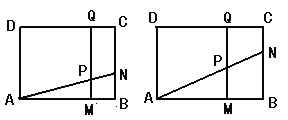
(1)若![]() 厘米,
厘米,![]() 秒,求PM的长度;
秒,求PM的长度;
(2)若![]() 厘米,求出某个时间
厘米,求出某个时间![]() ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求![]() 的取值范围;
的取值范围;
【答案】(1)![]() (2)
(2)![]() ,使
,使![]() ,相似比为
,相似比为![]()
(3)![]() ,
,
【解析】
(1)容易知道△ANB∽△APM,利用相似三角形的对应边成比例就可以求出PM;
(2)若PNB∽△PAD,则![]() ,而
,而![]() ,∴
,∴![]() ,则可求出t,也可以求出相似比;
,则可求出t,也可以求出相似比;
(3)首先用△AMP∽△ABN把QM,PM用t表示,再用t表示梯形PMBN与梯形PQDA的面积,根据已知可以得到关于t的方程,再由t与a的关系式可以求t的取值范围了;
(4)由(3)根据梯形PQCN的面积与梯形PMBN的面积相等得到关于t的方程,求出t,再求出a,则问题可解.
解:(1)当t=1时,MB=1,NB=1,AM=4-1=3,
∵PM∥BN
∴△ANB∽△APM,
∴![]() ,
,
∴PM=![]()
(2)当t=2时,使△PNB∽△PAD,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]()
解得t=2,则相似比为2:3.
(3)![]() ,
,
⊿APM∽⊿ABN ,
![]() ,
,
即:![]()
∴![]()
当梯形![]() 与梯形
与梯形![]() 的面积相等,即
的面积相等,即![]()
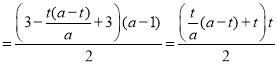
化简得![]() ,
,
![]() ,
,
![]() ,
,
则![]() ,
,


科目:初中数学 来源: 题型:
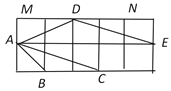
【题目】如图,在2×2的正方形网格中,小正方形的边长均为1,△ABC与△ADE的顶点都在格点上.
(1)求证:△ABC∽△ADE;
(2)求∠MDA+∠NDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
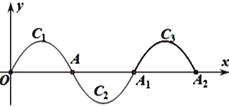
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了改善居住环境,准备修建一个巨型花园ABCD,为了节约材料并种植不同花卉,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块.已知所用栅栏的总长为60米,墙长为30米,设花园垂直于墙的一边的长为![]() 米.
米.

(1)若平行于墙的一边长为![]() 米,直接写出
米,直接写出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
(3)当这个花园的面积不小于288平方米时,试结合函数图象,直接写出![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
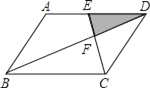
A. 8S B. 9S C. 10S D. 11S
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如表:
原科维生素C及价格 | 甲种原料 | 乙种原料 |
维生素c(单位/千克) | 600 | 400 |
原料价格(元/千克) | 9 | 5 |
现要配制这种营养食品20千克,设购买甲种原料x千克,购买这两种原料的总费用为y元.
(1)求y与x的函数关系式?
(2)若食堂要求营养食品每千克至少含有480单位的维生素C,试说明需要购买甲种原料多少千克时,总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足即将到来的春节市场需求,某超市购进一种品牌的食品,每盒进价为30元,根据往年的销售经验发现:当售价定为每盒50元时,每天可卖出100盒,每降价1元,每天可多卖出10盒,超市规定售价不低于40元/盒,不高于50元/盒.
(1)求每天的销售利润W(元)与每盒降价x(元)之间的函数关系式(注明自变量的取值范围);
(2)当每盒售价为多少元时,每天的销售利润最大?
(3)若要使每天的销售利润不低于2090元,那么每盒的售价应定在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
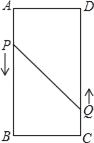
【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?
(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com