
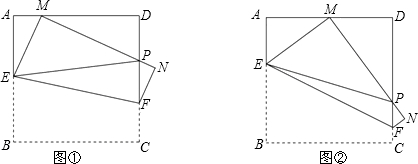
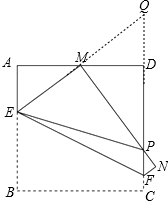
 解:(1)由折叠知BE=EM,∠B=∠EMP=90°.
解:(1)由折叠知BE=EM,∠B=∠EMP=90°.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| C△PDM |
| C△MAE |
| MD |
| AE |
| MD |
| AE |
| 4-x | ||
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 (2013•江宁区二模)在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),将△ABC绕点A逆时针旋转90°,则在△ABC扫过的区域中(不含边界上的点),到点O的距离为无理数的格点的个数是( )
(2013•江宁区二模)在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),将△ABC绕点A逆时针旋转90°,则在△ABC扫过的区域中(不含边界上的点),到点O的距离为无理数的格点的个数是( )查看答案和解析>>
科目:初中数学 来源: 题型:单选题
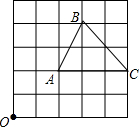 在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),将△ABC绕点A逆时针旋转90°,则在△ABC扫过的区域中(不含边界上的点),到点O的距离为无理数的格点的个数是
在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),将△ABC绕点A逆时针旋转90°,则在△ABC扫过的区域中(不含边界上的点),到点O的距离为无理数的格点的个数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com