
分析 (1)把a看做已知数表示出方程组的解,根据x与y同号求出a的范围即可;
(2)由a的范围判断绝对值里边式子的正负,利用绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)$\left\{\begin{array}{l}{x+y=5+a①}\\{2x-y=1-4a②}\end{array}\right.$,
①+②得:3x=6-3a,即x=2-a,
代入①得:y=3+2a,
根据题意得:xy=(2-a)(3+2a)>0,
解得-$\frac{3}{2}$<a<2;
(2)∵-$\frac{3}{2}$<a<2,
∴当-$\frac{3}{2}$<a<0时,|2a+3|+2|a|=2a+3-2a=3;
当0≤a<2时,|2a+3|+2|a|=2a+3+2a=4a+3.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
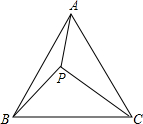 数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断
数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小华想知道线段AB和DF是否平行,但是他只带了一个三角板,于是他想了这样一个办法.
小华想知道线段AB和DF是否平行,但是他只带了一个三角板,于是他想了这样一个办法.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
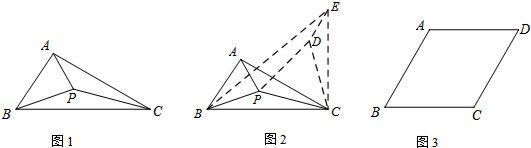
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com