
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点A作直线l,若直线l与两坐标轴围成的三角形面积为8,请直接写出满足条件的直线l的条数.
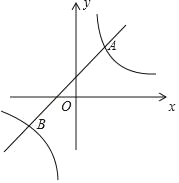
【答案】(1)y=![]() ,y=x+1;(2)x>2或﹣3<x<0;(3)满足条件的直线l有两条.
,y=x+1;(2)x>2或﹣3<x<0;(3)满足条件的直线l有两条.
【解析】
(1)根据一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点,可以求得一次函数与反比例函数的解析式;
的图象相交于A(2,3),B(﹣3,n)两点,可以求得一次函数与反比例函数的解析式;
(2)根据题目中的条件和函数图象可以直接写出不等式kx+b>![]() 的解集;
的解集;
(3)根据题意可以求出满足条件的直线l,本题得以解决.
(1)∵反比例函数y=![]() 的图象过点A(2,3),B(﹣3,n),
的图象过点A(2,3),B(﹣3,n),
∴3=![]() ,得m=6,
,得m=6,
∴反比例函数的解析式为y=![]() ,
,
∴n=![]() =﹣2,
=﹣2,
即点B的坐标为(﹣3,﹣2),
∵一次函数y=kx+b过点A(2,3),B(﹣3,﹣2),
∴![]() ,得
,得![]() ,
,
即一次函数的解析式为y=x+1;
(2)∵一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点,
的图象相交于A(2,3),B(﹣3,n)两点,
∴不等式kx+b>![]() 的解集是x>2或﹣3<x<0;
的解集是x>2或﹣3<x<0;
(3)满足条件的直线l有两条,
理由:设直线l的解析式为y=mx+n,
当x=0时,y=n,当y=0时,x=![]() ,
,
即直线l与x轴的交点为(![]() ,0),与y轴的交点为(0,n),
,0),与y轴的交点为(0,n),
∵点A(2,3)在直线l上,
∴2m+n=3,得n=3﹣2m,
∵直线l与两坐标轴围成的三角形面积为8,
∴当m>0时,![]() ,
,
解得,m=±![]() ,
,
当m<0时,![]() ,此时无解,
,此时无解,
故满足条件的直线l有两条.


科目:初中数学 来源: 题型:
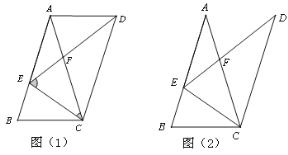
【题目】在△ABC中,AB=AC,BC=2,将△ABC绕点C顺针方向旋转α(0°<α<360°),得到△DEC,使点E在AB边上。
(1)如图1,连接AD,
①求证:四边形ABCD是平行四边形;
② 当AE=AD时,求旋转角α的度数;
(2)如图2,若AE=2BE,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
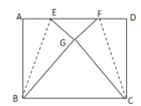
【题目】如图,在矩形ABCD中,2AB>BC,点E和点F为边AD上两点,将矩形沿着BE和CF折叠,点A和点D恰好重合于矩形内部的点G处,
(1)当AB=BC时,求∠GEF的度数;
(2)若AB=![]() ,BC=2,求EF的长.
,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“两会”知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验.
①收集数据:分别记录甲、乙两名学生10次测验成绩(单位:分)
次数 成绩 学生 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 | 74 | 84 | 89 | 83 | 86 | 81 | 86 | 84 | 86 | 86 |
乙 | 82 | 73 | 81 | 76 | 81 | 87 | 81 | 90 | 92 | 96 |
②整理数据:两组数据的平均数、中位数、众数、方差如下表所示:
统计量 学生 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 83.9 | ______ | 86 | 15.05 |
乙 | 83.9 | 81.5 | ______ | 46.92 |
③分析数据:根据甲、乙两名学生10次测验成绩绘制折线统计图:
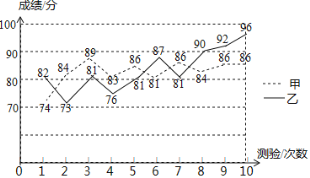
④得出结论:结合上述统计全过程,回答下列问题:
(1)补全②中的表格.
(2)判断甲、乙两名学生中, (填甲或乙)的成绩比较稳定,说明判断依据: .
(3)如果你是决策者,从甲、乙两名学生中选择一人代表学校参加知识竞赛,你会选择______(填“甲”或“乙),理由是:____ __.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )
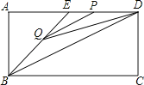

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线 x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)方程a(x﹣1)2 + b(x﹣1)+c=0的两根是x1= 0,x2= 6.其中正确的结论有( )
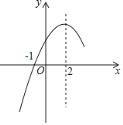
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,若y与x之间的函数关系图象如图2所示,当x=6时,PQ的值是( )
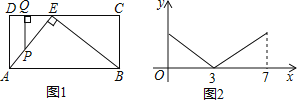
A. 2B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() ,点
,点![]() ,点
,点![]() ,动点
,动点![]() 在直线
在直线![]() 上,动点
上,动点![]() 、
、![]() 在
在![]() 轴正半轴上,连接
轴正半轴上,连接![]() 、
、![]() 、
、![]() .
.
(1)若点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
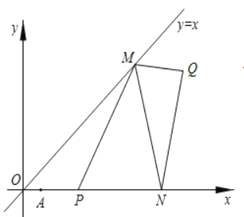
(2)如图![]() ,当
,当![]() 周长最小时,连接
周长最小时,连接![]() ,求
,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
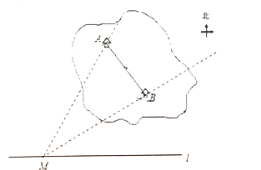
【题目】小强想知道湖中两个小亭A、B之间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道I上某一观测点M处,测得亭A在点M的北偏东30°,亭B在点M的北偏东60°,当小明由点M沿小道I向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小强计算湖中两个小亭A、B之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com