
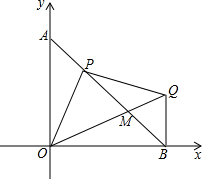
 已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:
已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:分析 (1)根据题意得△OAB是等腰直角三角形,再证明O、P、Q、B四点共圆,得出∠OBP=∠OQP=45°,即可得出△OPQ是等腰直角三角形;
(2)以OM为对称轴,作OB的轴对称图形得OB′,连接PB′,则△OBM≌△OB′M,得出BM=B′M,∠OBM=∠OB′M=45°,再证明△AOP≌△B′OP,得出AP=B′P,∠OAP=∠OB′P=45°,证出△PB′M是直角三角形,即可得出结论;
(3)先求出直线AB的解析式为:y=-x+4,设点P的坐标为(a,4-a),由勾股定理得OP2+PQ2=OQ2,得出2[a2+(4-a)2]=42+BQ2,解得,BQ2=(2a-4)2,当点P运动至AB的中点时,点Q与点B重合,不合题意,得出a<2,BQ=4-2a,由$\sqrt{2}$BP-BQ=(8-2a)-(4-2a)=4,即可得出结论,定值为4.
解答 解:(1)△OPQ是等腰直角三角形;理由如下:
∵A(0,4),B(4,0),
∴OA=OB,
∴△OAB是等腰直角三角形,
∵OP⊥PQ,BQ⊥x轴,
∴∠OPQ=∠OBQ=90°,
∴∠OPQ+∠OBQ=180°,
∴O、P、Q、B四点共圆,
∴∠OBP=∠OQP=45°(同弧所对的圆周角相等),
∴△OPQ是等腰直角三角形;
(2)PM2=BM2+AP2,AP、PM、BM成勾股关系;理由如下:
以OM为对称轴,作OB的轴对称图形得OB′,连接PB′,如图所示: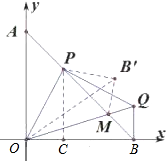 ∵OB和OB′关于OM对称,
∵OB和OB′关于OM对称,
∴△OBM≌△OB′M,
∴BM=B′M,∠OBM=∠OB′M=45°,
由(1)知∠POQ=45°,
∴∠AOP+∠BOM=45°,
又∠BOM=∠B′OM,∠B′OP+∠B′OP=45°,
∴∠AOP=∠B′OP,OA=OB′=4,OP=OP,
∴△AOP≌△B′OP,
∴AP=B′P,∠OAP=∠OB′P=45°,
∴△PB′M是直角三角形,
∴PM2=B′M2+B′P2,即PM2=BM2+AP2,
∴AP、PM、BM成勾股关系;
(3)不发生变化;理由如下:设直线AB的解析式为y=kx+b,
把A(0,4),B(4,0)代入得:$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$,
解得:k=-1,b=4,
∴直线AB的解析式为:y=-x+4,
∴设点P的坐标为(a,4-a),
∴$\sqrt{2}$BP=$\sqrt{2}×\sqrt{2}$(4-a)=8-2a,
∵OP2+PQ2=OQ2,
∴2OP2=OB2+BQ2,
∴2[a2+(4-a)2]=42+BQ2,
解得,BQ2=(2a-4)2,
∵当点P运动至AB的中点时,点Q与点B重合,
∴不合题意,
∴a<2,
∴BQ=4-2a,
∴$\sqrt{2}$BP-BQ=(8-2a)-(4-2a)=4,
∴$\sqrt{2}$BP-BQ的值没有发生变化,定值为4.
点评 本题考查了坐标与图形性质、等腰直角三角形的性质与判定、直角三角形的判定、一次函数解析式的确定、勾股定理;本题难度较大、综合性强,特别是(2)(3)中,需要通过作辅助线才能得出结论.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
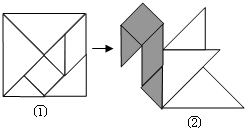 用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )| A. | 12 | B. | 16 | C. | 18 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,对角线AC、BD相交于点O,且AB=AD,OB=OD,下列结论:①BC=DC;②AC⊥BD;③AC平分∠BAD;④△AOB≌△COD;⑤∠ABC=∠ADC,其中正确的是①②③⑤(只需填序号).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且AB=AD,OB=OD,下列结论:①BC=DC;②AC⊥BD;③AC平分∠BAD;④△AOB≌△COD;⑤∠ABC=∠ADC,其中正确的是①②③⑤(只需填序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com