
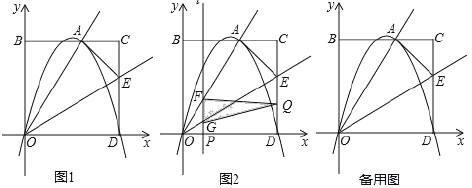
【题目】如图1,矩形OBCD的边OD,OB分别在x轴和y轴上,且B (0,8),D(10,0).点E是DC边上一点,将矩形OBCD沿过点O的射线OE折叠,使点D恰好落在BC边上的点A处.
(1)若抛物线y=ax2+bx经过点A,D,求此抛物线的解析式;
(2)若点M是(2)中抛物线对称轴上的一点,是否存在点M,使△AME为等腰三角形?若存在,直接写出点M的坐标;若不存在,说明理由;
(3)如图2,动点P从点O出发沿x轴正方向以每秒1个单位的速度向终点D运动,动点Q从点D出发沿折线D﹣C﹣A以同样的速度运动,两点同时出发,当一点运动到终点时,另一点也随之停止,过动点P作直线1⊥x轴,依次交射线OA,OE于点F,G,设运动时间为t(秒),△QFG的面积为S,求S与t的函数关系式,并直接写出t的取值范围.(t的取值应保证△QFG的存在)
【答案】(1)![]() ;(2)存在,满足要求的点M的坐标为
;(2)存在,满足要求的点M的坐标为![]() ,(5,5),(5,2.5),理由见解析;(3)
,(5,5),(5,2.5),理由见解析;(3)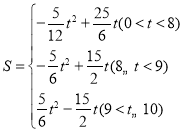
【解析】
(1)先利用矩形的性质及折叠的性质求出点A的坐标,然后用待定系数法即可求得抛物线的解析式;
(2)易求得抛物线的对称轴x=5,过点E作ET⊥AH,垂足为T,设点M的坐标为(m,n),运用勾股定理用含n的代数式表示出AM2、EM2,然后分三种情况进行讨论:AM=AE, EM=EA, MA=ME分别列出等式,求出n,就可求出点M的坐标;
(3)根据点Q的位置不同,分以下四种情况进行讨论:①点Q在线段DC上;②点Q在AC上且在直线l的右边;③点Q在AC上且在直线l上;④点Q在AC上且在直线l的左边,分情况讨论即可.
(1)解:∵四边形OBCD是矩形,B(0,8),D(10,0),
∴BC=OD=10,DC=OB=8,∠OBC=∠C=90°.
由折叠可得:OA=OD=10,AE=DE.
∵∠OBC=90°,OB=8,OA=10,
∴AB=![]() ,
,
∴AC=4.
设AE=DE=x,则CE=8﹣x,
∵∠C=90°,
∴x2=42+(8﹣x)2,
解得:x=5,
∴AE=DE=5,
∴点A的坐标为(6,8),点E的坐标为(10,5).
∵抛物线y=ax2+bx经过点A(6,8),D(10,0),
∴![]() 解得
解得
此抛物线的解析式为![]() ;
;
(2)存在M,使△AME为等腰三角形.
设抛物线的对称轴与BC交于点H,过点E作ET⊥AH,垂足为T,连接AM、ME,如图1,
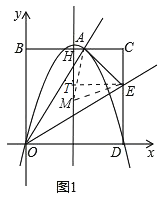
设点M的坐标为(m,n),则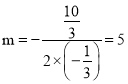 ,
,
∴AH=6﹣5=1,HM=8﹣n,ET=10﹣5=5,TM=5﹣n
∵AH⊥HM,
∴AM2=AH2+MH2=1+(8﹣n)2
∵ET⊥MH
∴ME2=ET2+MT2=25+(5﹣n)2
①若AM=AE,则AM2=AE2,
∴1+(8﹣n)2=25,
∴(8﹣n)2=24,
解得:![]() ,
,
此时点M的坐标为![]() 或
或 ![]() ;
;
②若EM=EA,则EM2=EA2
∴25+(5﹣n)2=25
∴(5﹣n)2=0
∴n3=5
此时点M的坐标为![]() ;
;
③若MA=ME,则MA2=ME2
∴1+(8﹣n)2=25+(5﹣n)2
解得:n4=2.5
此时点M的坐标为![]() ;
;
综上所述:满足要求的点M的坐标为![]() ,(5,5),(5,2.5);
,(5,5),(5,2.5);
(3)设直线OA的解析式y=k1x,
∵点A的坐标为(6,8),
∴6k1=8,
∴![]() ,
,
∴直线OA的解析式为![]() ,
,
同理可得:直线OE的表达式为y=![]() ,
,
∵OP=1×t=t
∴P(t,0)
∵直线l⊥x轴于点P,点F,G是直线l与OA,OE的交点
∴![]() ,
,
故![]() ,
,
①当0<t<8时,点Q在线段DC上,
过点Q作QS⊥直线l,垂足为S,
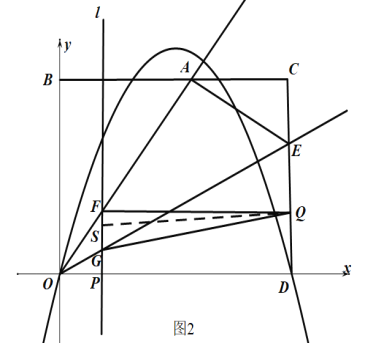
则QS=PD=10﹣t
∴![]()
=![]()
=![]() ;
;
②当8≤t<9时,点Q在线段CA上,且在直线l的右侧,
设FG交AC于点N,如图3,
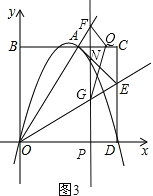
则QN=CN﹣CQ=PD﹣CQ=(10-t)﹣(t﹣8)=18﹣2t
∴![]()
=![]()
=![]() ;
;
③当t=9时,QN=18﹣2t=0,点Q与点N重合,此时△QFG不存在,故舍去;
④当9<t≤10时,点Q在线段CA上,且在直线l的左侧,设FG交AC于点N,如图4.
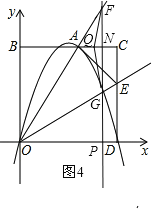
则QN=CQ﹣CN=CQ﹣PD=(t-8)-(10-t)=2t﹣18
∴![]()
=![]()
=![]() ;
;
综上所述: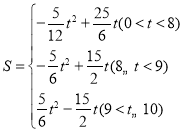 .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
(1)如图1,若将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() 连接
连接![]() 则
则![]() 的面积;
的面积;
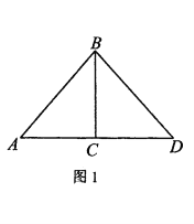
(2)如图2,点![]() 为
为![]() 延长线上一个动点,连接
延长线上一个动点,连接![]() 以
以![]() 为直角项点,
为直角项点,![]() 为直角边作等腰直角
为直角边作等腰直角![]() 连接
连接![]() ,求证:
,求证:![]() ;
;
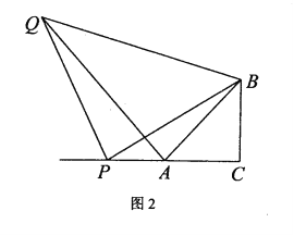
(3)如图3,点![]() 为线段
为线段![]() 上两点,且
上两点,且![]() 点
点![]() 是线段
是线段![]() 上一个动点,点
上一个动点,点![]() 是线段
是线段![]() 上一个动点,是否存在点
上一个动点,是否存在点![]() 使
使![]() 的值最小,若存在,求出最小值;若不存在,说明理由.
的值最小,若存在,求出最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会为了解本校学生每天做作业所用的时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案:
(A)对各班班长进行调查;
(B)对某班的全体学生进行调查;
(C)从全校每班随机抽取5名学生进行调查.
在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会收集到的数据整理后绘制成如图所示的条形统计图.

(1)为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案____(填A或B或C);
(2)被调查的学生每天做作业所用的时间的众数为_______小时,中位数为______小时;
(3)根据以上统计结果,估计该校800名学生中每天做作业时间用1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD 是菱形ABCD 的对角线,∠A=30°.
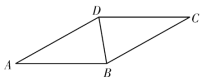
(1)请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,求∠DBF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
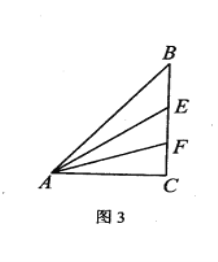
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
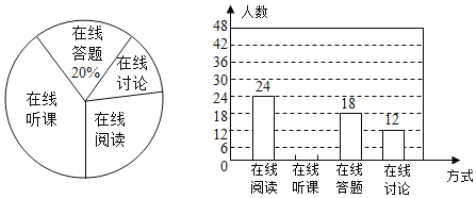
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生2700人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=4,求△OEC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com