
【题目】在△ABC中,点D是AB边上一点(不与AB重合),AD=kBD,过点D作∠EDF+∠C=180°,与CA、CB分别交于E、F.
(1)如图1,当DE=DF时,求![]() 的值.
的值.
(2)如图2,若∠ACB=90°,∠B=30°,DE=m,求DF的长(用含k,m的式子表示)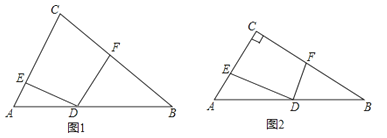
【答案】解:(1)如图1,连接CD,
∵∠EDF+∠C=180°,
∴D,E,C,F四点共圆,
∵DE=DF,
∴∠DCE=∠DCF,
根据正弦定理得![]() ①,
①,![]() ,
,
∴![]() ,②,
,②,
∵∠ADC=180°﹣∠BDC,
∴sin∠ADC=sin∠BDC,
①÷②d得,![]() ,
,
∵AD=kBD,
∴![]() =k;
=k;
(2)∵∠ACB=90°,∠B=30°,
∴∠A=60°,
根据正弦定理得:![]() ③,
③,![]() ,④,
,④,
由(1)知D,E,C,F四点共圆,
∴∠DEA+∠DFB=180°,
∴sin∠DEA=sin∠DFB,④÷③得:![]() ,
,
∴DF=![]() ,
,
∵AD=kBD,DE=m,
∴DF=![]() .
.
【解析】(1)连接CD,由∠EDF+∠C=180°,推出D,E,C,F四点共圆,根据正弦定理得![]() ①,
①,![]() , ②,①÷②得,
, ②,①÷②得,![]() , 根据AD=kBD,根据得到结论;
, 根据AD=kBD,根据得到结论;
(2)根据三角形的内角和得到∠A=60°,根据正弦定理得:![]() ③,
③,![]() , ④,④÷③得:
, ④,④÷③得:![]() , 求得DF=
, 求得DF=![]() , 即可得到结论.
, 即可得到结论.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( ) 
A.4米
B.2米
C.1.8米
D.3.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别,随机从箱子里取出1个球,放回搅匀再取一次,请你用画树状图或列表的方法表示所有可能出现的结果,求两次取出的都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形且![]() ,求∠B的大小.
,求∠B的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com