
【题目】P是抛物线y=x2-4x+5上一点,过点P作PM⊥x轴,PN⊥y轴,垂足分别是M,N,则PM+PN的最小值是( )
A.3B.![]() C.
C.![]() D.5
D.5
【答案】B
【解析】
设点P的坐标为(m, m2-4m+5) ,构造出PM+ PN的值与m的函数关系,利用二次函数的性质解决问题即可.
抛物线y=x2 -4x+5,△=16-20=-4<0,可知抛物线的值恒为正,
设P(m,m2-4m+5) ,
则PM=|m2 - 4m+5|,PN=|m|
当m<0时, PM+ PN=|m2- 4m+5|+|m|= m2 - 4m+5-m= m2-5m+ 5=![]() ,
,
此时m=![]() 不符合m<0;
不符合m<0;
当m=0时,y=5,PM+ PM的值是5;
当m>0时,PM+ PN=|m2 - 4m+ 5|+|m|=m2 -4m+5+m=m2-3m + 5=![]() ,
,
所以当m=![]() 时, PM+ PM的最小值为
时, PM+ PM的最小值为![]() ,
,
综上,PM+ PM的最小值是![]()
故答案为:B


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点E是AD的中点,连接CE,并延长CE与BA的延长线交于点F, 若∠BCF=90°,则∠D的度数为( )
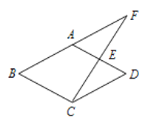
A.60°B.55°C.45°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到下表数据:
x | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 6 | 12 |
y | 12 | 6 | ■ | 3 | 2 | 1.5 | 1 | 0.5 |
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_________;
(2)y与x的函数关系式为_________,且y随x的增大而_________;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形![]() 的面积记为
的面积记为![]() ,矩形
,矩形![]() 的面积记为
的面积记为![]() ,请判断
,请判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
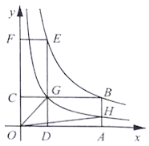
(4)在(3)的条件下,![]() 交
交![]() 于点G,反比例函数
于点G,反比例函数![]() 的图象经过点G交
的图象经过点G交![]() 于点H,连接
于点H,连接![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为_________.
的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.

(1)判断AF和⊙O的位置关系并说明理由.
(2)若∠ABC=60°,BC=1cm,求阴影部分的面积.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x60 | x |
售价(元/件) | 200 | 100 |
若用1800元购进甲种商品的件数与用900元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共100件,其中销售甲种商品为a件(a40),设销售完100件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
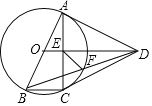
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=![]() cm.
cm.
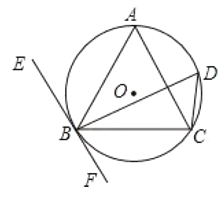
(1)请探究EF与⊙O的位置关系,并说明理由;
(2)求⊙O的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
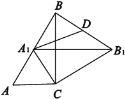
【题目】如图,RtΔABC中∠C=90°,∠ABC=30°,ΔABC绕点C顺时针旋转得ΔA1B1C,当A1落在AB上时,连接B1B,取B1B的中点D,连接A1D,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com