

分析 过C点作FG⊥AB于F,交DE于G.在Rt△ACF中,根据三角函数可求CF,则CG=h-CF,然后在Rt△CDG中,根据三角函数可求CD的长度.
解答 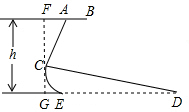 解:过C点作FG⊥AB于F,交DE于G.
解:过C点作FG⊥AB于F,交DE于G.
∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,
∴∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+12°-80°=22°,
∴∠CAF=68°,
在Rt△ACF中,CF=AC•sin∠CAF=0.8•sin68°≈0.744(m),
则CG=h-CF=1.1-0.744=0.356(m).
在Rt△CDG中,CD=$\frac{CG}{sin∠CDE}$=$\frac{0.356}{sin12°}$≈$\frac{0.356}{0.21}$=1.7(m),
跑步机踏板CD的长度约为1.7m.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键是用数学知识解决实际问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
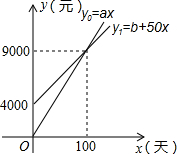 国家推行“节能减排,低碳经济“的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时间(单位:天)之间分别满足关系式:y0=ax,y1=b+50x,如图所示,试根据图象解决下列问题:
国家推行“节能减排,低碳经济“的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时间(单位:天)之间分别满足关系式:y0=ax,y1=b+50x,如图所示,试根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 2 | 5 | 13 | 10 | 7 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 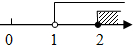 | B. | 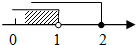 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 球数/个 | 6 | 7 | 8 | 9 | 10 | 12 |
| 人数 | 1 | 1 | 1 | 4 | 3 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 根据图中数据,计算大长方形的面积,通过不同的计算方法,你发现的结论是( )
根据图中数据,计算大长方形的面积,通过不同的计算方法,你发现的结论是( )| A. | (a+b)(a+2b)=a2+3ab+2b2 | B. | (3a+b)(a+b)=3a2+4ab+b2 | ||
| C. | (2a+b)(a+b)=2a2+3ab+b2 | D. | (3a+2b)(a+b)=3a2+5ab+2b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com