
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )

A. ∠2 B. ∠3 C. ∠4 D. ∠5
D 【解析】【解析】 ∠1的同位角是∠5, 故选:D.科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
某商品原价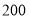 元,连续两次降价后售价为
元,连续两次降价后售价为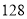 元,若设两次降价的平均降价率为
元,若设两次降价的平均降价率为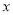 ,则下列所列方程,正确的是( ).
,则下列所列方程,正确的是( ).
A. 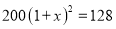 B.
B. 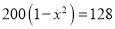 C.
C.  D.
D. 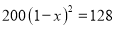
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:单选题
多项式x2﹣2xy3﹣ y﹣1是( )
y﹣1是( )
A. 三次四项式 B. 三次三项式 C. 四次四项式 D. 四次三项式
C 【解析】试题解析:多项式x2-2xy3-y-1有四项,最高次项-2xy3的次数为四,是四次四项式. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:解答题
如果∠A与∠B的两条边分别平行,其中∠A=(x+30)°;∠B =(3x-10)°,那么∠A的度数为________
50°或70° 【解析】(1)如图(1) 由题意知:AM//BE,AN//BF, ∴∠A=∠1=(x+30)°,∠2+∠B=180° 又∠1=∠2,∴∠2=∠A=(x+30)°, 又∠B=(3x-10)°, ∴ ,解得x=40, ∴∠A=(40+30)°=70°. (2)如图(2,), 由题意知:AM//BE,AN//BF, ∴∠1=∠A...查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:单选题
已知∠1与∠2是直线a与直线b被直线c所截得的内错角,且有∠1=50°,则∠2=( )
A. 130° B. 50° C. 80° D. 无法确定
D 【解析】如图, ∵直线a,b位置不确定,可能相交,也可能平行, 而∠1与∠2是内错角关系,两者可能相等,也可能不等, ∴∠2的大小也不确定. 故答案选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:解答题
体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢球后,足球踢到了小华处的概率是多少(用树状图或列表的方法加以说明)?
(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
(1)(2)应从小明开始踢 【解析】试题分析:(1)列举出所有情况,看足球踢到了小华处的情况数占所有情况数的多少即可; (2)可设球从小明处先开始踢,得到3次踢球回到小明处的概率,进而根据树状图可得球从其他2位同学处开始,3次踢球回到小明处的概率,比较可得可能性最小的方案. 试题解析:(1)如图: ∴P(足球踢到小华处)= (2)应从小明开始踢如图: 若从小明开...查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:填空题
甲、乙、丙三位同学打乒乓球,想通过“手心手背”游戏来决定其中哪两人先打.规则如下:三人同时各用一只手随机出示手心或手背,若只有两人手势相同(都是手心或都是手背),则这两人先打;若三人手势相同,则重新决定.那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是_________.
【解析】试题解析:分别用A、a表示手心和手背, 画树状图为: 共有8种等可能的结果数,其中甲打乒乓球的结果数为4, 所以通过一次“手心手背”游戏能决定甲打乒乓球的概率=. 故答案为: .查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:单选题
在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:填空题
若二次根式 有意义,则x的取值范围为__________。
有意义,则x的取值范围为__________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com