
【题目】已知抛物线y=ax2+bx+c经过A(0,2),B(2,﹣2)两点.
⑴用含a的式子表示b.
⑵当a=﹣![]() 时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
⑶若a>0,线段AB下方的抛物线上有一点E,求证:不管a取何值,当△EAB的面积最大时,E点的横坐标为定值.
【答案】(1)b=﹣2a﹣2;(2)x=﹣2或x=0或x=-1+![]() 或x=-1-
或x=-1-![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)利用待定系数法建立方程组求解即可得出结论;
(2)先求出抛物线解析式,配方得:y=![]() ,由y是正整数,得出(x+1)2=1或(x+1)2=3,解方程即可得出结论;
,由y是正整数,得出(x+1)2=1或(x+1)2=3,解方程即可得出结论;
(3)根据三角形的面积的计算方法建立函数关系式,即可得出结论.
(1)∵抛物线y=ax2+bx+c经过A(0,2),B(2,﹣2),∴![]() ,∴
,∴![]() ,即:b=﹣2a﹣2;
,即:b=﹣2a﹣2;
(2)由(1)知,c=2,b=﹣2a﹣2.
∵a![]() ,∴b=﹣1,∴抛物线解析式为y
,∴b=﹣1,∴抛物线解析式为y![]() x2﹣x+2
x2﹣x+2![]() (x+1)2
(x+1)2![]() =
=![]() .
.
∵y=ax2+bx+c的函数值为正整数,即![]() 为正整数,∴(x+1)2=1或(x+1)2=3,解得:x=﹣2或x=0或x=-1+
为正整数,∴(x+1)2=1或(x+1)2=3,解得:x=﹣2或x=0或x=-1+![]() 或x=-1-
或x=-1-![]() ;
;
(3)由(1)知,c=2,b=﹣2a﹣2,∴抛物线的解析式为y=ax2﹣(2a+2)x+2.
∵A(0,2),B(2,﹣2),∴直线AB的解析式为y=﹣2x+2.
∵点E在线段AB下方的抛物线上,设点E(m,am2﹣(2a+2)m+2),过点E作y轴的平行线,交AB于F,∴F(m,﹣2m﹣2),∴EF=﹣2m﹣2﹣[am2﹣(2a+2)m+2]=﹣a(m﹣1)2+a,∴S△EAB![]() EF×|xB﹣xA|=EF=﹣a(m﹣1)2+a.
EF×|xB﹣xA|=EF=﹣a(m﹣1)2+a.
∵a>0,∴﹣a<0,∴m=1时,△EAB面积最大,即:不管a取大于0的何值,当△EAB的面积最大时,E点的横坐标为定值,定值为1.


科目:初中数学 来源: 题型:
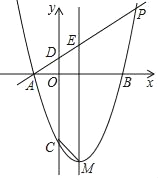
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
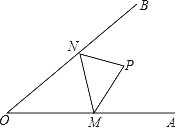
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
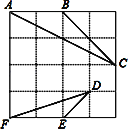
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
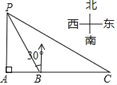
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>kx+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
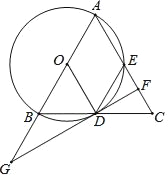
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC,AC于D,E两点,过点D作⊙O的切线,交AC于点F,交AB的延长线于点G.
(1)求证:EF=CF;
(2)若cos∠ABC=![]() ,AB=10,求线段AF的长.
,AB=10,求线段AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com