
 用火柴棒按下列方式搭建三角形:
用火柴棒按下列方式搭建三角形:| 三角形个数 | 1 | 2 | 3 | 4 | … |
| 火柴棒根数 | 3 | 5 | 7 | 9 | … |
分析 (1)按照图中火柴的个数填表即可;
(2)当三角形的个数为:1、2、3、4时,火柴棒的个数分别为:3、5、7、9,由此可以看出三角形的个数每增加一个,火柴棒的个数增加2根,所以当三角形的个数为n时,三角形个数增加n-1个,那么此时火柴棒的个数应该为:3+2(n-1);
(3)当n=1000时,直接代入(2)所求的规律中即可.
解答 解:(1)由图可知:
该表中应填的数依次为:3、5、7、9
(2)当三角形的个数为1时,火柴棒的根数为3;
当三角形的个数为2时,火柴棒的根数为5;
当三角形的个数为3时,火柴棒的根数为7;
当三角形的个数为4时,火柴棒的根数为9;
…
由此可以看出:每当三角形的个数增加1个时,火柴棒的个数相应的增加2,
所以,当三角形的个数为n时,火柴棒的根数为3+2(n-1)=2n+1.
(3)当n=1008时,2n+1=2017.
答:当n=1008时,火柴棒的根数是2017.
点评 此题考查了规律型:图形的变化类,本题解题关键根据第一问的结果总结规律,得到规律:三角形的个数每增加一个,火柴棒的个数增加2根,然后由此规律解答第三问.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:选择题
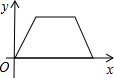 如图,是张老师晚上出门散步时离家的距离y与时间x之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
如图,是张老师晚上出门散步时离家的距离y与时间x之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )| A. | 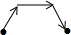 | B. |  | C. | 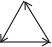 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com