
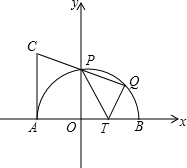
 如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.
如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.分析 (1)连接OQ,过点Q作QD⊥AB,垂足为D.由Q恰为弧PB中点可知OQ为∠POB的平分线,然后利用特殊锐角三角函数可求得点Q的坐标;
(2)由点P与点Q的坐标求得直线PC的解析式,然后将点C的横坐标代入解析式可求得点C的纵坐标,然后根据AC=AT从而可求得点T的横坐标,从而求得a的值;
(3)先求得TD的长,然后利用锐角三角函数的定义求得tan∠PTO=∠QTD,从而可知点由点P发出的光线,经过T的反射后,反射光线通过点Q.
解答 解:(1)连接OQ,过点Q作QD⊥AB,垂足为D.
∵Q恰为弧PB中点,
∴∠QOB=$\frac{1}{2}∠POB$=$\frac{1}{2}×90°$=45°.
∵OQ=2,
∴OD=OQ•cos45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,QD=OQ•sin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
∴点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
(2)设CP的解析式为y=kx+b.
根据题意得:$\left\{\begin{array}{l}{\sqrt{2}k+b=\sqrt{2}}\\{b=2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=1-\sqrt{2}}\\{b=2}\end{array}\right.$.
∴直线PC的解析式为y=(1-$\sqrt{2}$)x+2.
将x=-2代入直线的解析式为y=2$\sqrt{2}$.
∴AT=AC=2$\sqrt{2}$.
∴a=2$\sqrt{2}$-2.
(3)由(1)可知:OD=$\sqrt{2}$,QD=$\sqrt{2}$,由(2)可知:OT=2$\sqrt{2}-2$.
∴TD=$\sqrt{2}-$(2$\sqrt{2}-2$)=2-$\sqrt{2}$.
∴tan∠QTD=$\frac{QD}{TD}$=$\frac{\sqrt{2}}{2-\sqrt{2}}$=$\sqrt{2}+1$,tan∠PTO=$\frac{OP}{OT}$=$\frac{2}{2\sqrt{2}-2}$=$\sqrt{2}+1$.
∴∠QTD=∠PTO.
∴由点P发出的光线,经过T的反射后,反射光线能通过点Q.
点评 本题主要考查的是圆的综合应用,同时本题还考查的了锐角三角函数与待定系数法求函数的解析式,求得直线PC的解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
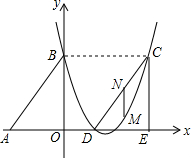 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}{x}^{2}+bx+c$经过B点,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}{x}^{2}+bx+c$经过B点,且顶点在直线x=$\frac{5}{2}$上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 480×108元 | B. | 4.8×1010元 | C. | 4.80×1010元 | D. | 4.80××108元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+b2=c2 | B. | b2+c2=a2 | C. | c2+a2=b2 | D. | b+a=c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
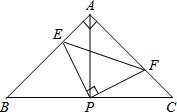 如图,在△ABC中,AB=AC=4,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,现给出以下四个结论:
如图,在△ABC中,AB=AC=4,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,现给出以下四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com