
 ��2013•������ģ�⣩һ��С�ͷ�ӳ����ӯ����yԪ����Ʊ��x��֮��Ĺ�ϵ��ͼ��ʾ������ͼ��õ����н�����ȷ�ĸ����У�������
��2013•������ģ�⣩һ��С�ͷ�ӳ����ӯ����yԪ����Ʊ��x��֮��Ĺ�ϵ��ͼ��ʾ������ͼ��õ����н�����ȷ�ĸ����У�������
|
|
|
|


 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
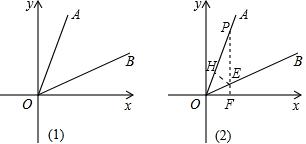
 ��2013•������ģ�⣩��ͼ��C��D��B������ֱ�Ϊ��1��0����9��0����10��0������P��t��0����CD��һ�����㣬��x���Ϸ����ȱߡ�OPE�͡�BPF����EF��GΪEF���е㣮
��2013•������ģ�⣩��ͼ��C��D��B������ֱ�Ϊ��1��0����9��0����10��0������P��t��0����CD��һ�����㣬��x���Ϸ����ȱߡ�OPE�͡�BPF����EF��GΪEF���е㣮| k |
| x |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| OH |
| PH |
| 1 |
| 2 |
| 1 |
| 2 |
| k-1 |
| k+1 |
| k+1 |
| 1-k |
| k-1 |
| k+1 |
| k+1 |
| 1-k |
| n |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•������ģ�⣩��ͼ��ƽ��ֱ������ϵ�У���A��0��4����B��3��0����D��E��x���ϣ�FΪƽ����һ�㣬��EF��x�ᣬֱ��DF��ֱ��AB���ഹֱ������ΪH����AOB�ա�DEF����BD=h��
��2013•������ģ�⣩��ͼ��ƽ��ֱ������ϵ�У���A��0��4����B��3��0����D��E��x���ϣ�FΪƽ����һ�㣬��EF��x�ᣬֱ��DF��ֱ��AB���ഹֱ������ΪH����AOB�ա�DEF����BD=h��| 36 |
| 5 |
| 36 |
| 5 |
| 37 |
| 7 |
| 7 |
| 12 |
| 5 |
| 12 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com