
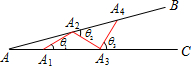
 如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.
如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.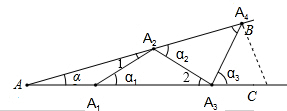 解:(1)小棒不能无限摆下去;
解:(1)小棒不能无限摆下去;
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| MT | RT |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.
如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为定值.上述结论有且只有一个是正确的,请选择你认为正确的结论度证明求值.
为定值.上述结论有且只有一个是正确的,请选择你认为正确的结论度证明求值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
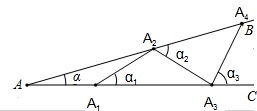 如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.
如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com