
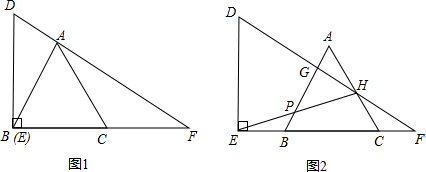
分析 (1)就是刚开始时C点与F的距离;
(2)①作EM⊥DF于点M,EN⊥AB于点N,证明△EBN≌△HAG即可;
②此时HEF是等腰三角形,作HP⊥EF于点P,由(1)知,EF=2AB,从而PE=AB=6,EH自然求出;
③由于前面已经证明了△EBN≌△HAG,从而有GH=EN,则△ENP≌△HGP,PG=NP=$\frac{1}{2}$AB.
解答 解:(1)等边△ABC未平移时,如图1,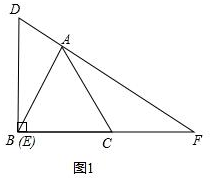
∵∠ABC=60°,BD⊥BF,
∴∠DBA=30°,
∵∠BDF=60°,
∴BA⊥DF,
∴2AB=BF=BC+CF,
∵AB=BC,
∴CF=AB=6,
即:点C平移到与点F重合时,等边△ABC平移的距离为6;
(2)
①作EM⊥DF于点M,EN⊥AB于点N,如图2,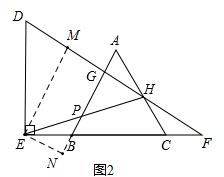
由(1)知AB⊥DF,
∴MENG是矩形,
∴GN=EM=AB,
∵∠ACB=60°,∠DFE=30°,
∴∠CHF=30°,
∴∠AHG=30°,
∵EN∥DF,
∴∠BEN=30°=∠AHG,
∵AG+GB=AB,
BN+GB=NG=AB,
∴BN=AG,
在△EBN和△HAG中,
$\left\{\begin{array}{l}{∠BEN=∠AHG}\\{∠ENB=∠AHG}\\{AG=BN}\end{array}\right.$,
∴△EBN≌△HAG(AAS),
∴EB=AH;
②如图3,作HP⊥EF于点P,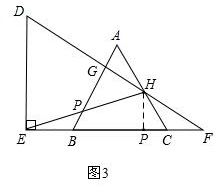
∵∠HEF=30°=∠HFE,
∴PE=PF,
由(1)知EF=2AB=12,
∴PE=6,
∴PH=$2\sqrt{3}$,
∴EH=4$\sqrt{3}$;
③不变.如图2,
∵△EBN≌△HAG,
∴GH=NE,
在△ENP和△HGP中,
$\left\{\begin{array}{l}{∠ENP=∠HGP}\\{∠EPN=∠HPG}\\{EN=HG}\end{array}\right.$,
∴△ENP≌△HGP(AAS),
∴GP=NP=$\frac{1}{2}$NG=$\frac{1}{2}AB$=3.
点评 本题考查了等边三角形的性质、含30度的直角三角形的性质、矩形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质等知识点,综合性较强,有一定难度.清楚AB等于点E到DF的距离且在平移过程中始终与DF垂直是作出辅助线的突破口和关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
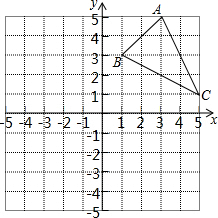 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
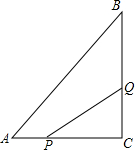 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com