
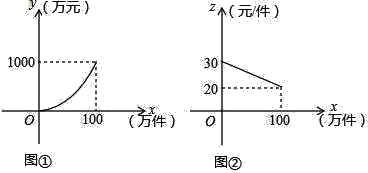
【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为W万元.(毛利润=销售额﹣生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;(写出自变量x的取值范围)
(2)求W与x之间的函数关系式;(写出自变量x的取值范围);并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
【答案】(1)y=![]() x2.z=﹣
x2.z=﹣![]() x+30(0≤x≤100);(2)年产量为75万件时毛利润最大,最大毛利润为1125万元;(3)今年最多可获得毛利润1080万元
x+30(0≤x≤100);(2)年产量为75万件时毛利润最大,最大毛利润为1125万元;(3)今年最多可获得毛利润1080万元
【解析】
(1)利用待定系数法可求出y与x以及z与x之间的函数关系式;(2)根据(1)的表达式及毛利润=销售额﹣生产费用,可得出w与x的函数关系式,再利用配方法求出最值即可;(3)首先求出x的取值范围,再利用二次函数增减性得出答案即可.
(1)图①可得函数经过点(100,1000),
设抛物线的解析式为y=ax2(a≠0),
将点(100,1000)代入得:1000=10000a,
解得:a=![]() ,
,
故y与x之间的关系式为y=![]() x2.
x2.
图②可得:函数经过点(0,30)、(100,20),
设z=kx+b,则![]() ,
,
解得: 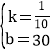 ,
,
故z与x之间的关系式为z=﹣![]() x+30(0≤x≤100);
x+30(0≤x≤100);
(2)W=zx﹣y=﹣![]() x2+30x﹣
x2+30x﹣![]() x2
x2
=﹣x2+30x
=﹣![]() (x2﹣150x)
(x2﹣150x)
=﹣![]() (x﹣75)2+1125,
(x﹣75)2+1125,
∵﹣![]() <0,
<0,
∴当x=75时,W有最大值1125,
∴年产量为75万件时毛利润最大,最大毛利润为1125万元;
(3)令y=360,得![]() x2=360,
x2=360,
解得:x=±60(负值舍去),
由图象可知,当0<y≤360时,0<x≤60,
由W=﹣![]() (x﹣75)2+1125的性质可知,
(x﹣75)2+1125的性质可知,
当0<x≤60时,W随x的增大而增大,
故当x=60时,W有最大值1080,
答:今年最多可获得毛利润1080万元.


科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
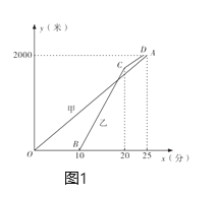
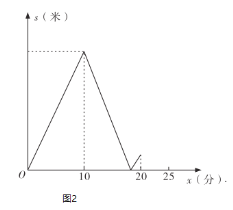
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(﹣![]() a6x5y4)÷(﹣3a2xy2)×(﹣
a6x5y4)÷(﹣3a2xy2)×(﹣![]() ax)2
ax)2
(3)[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
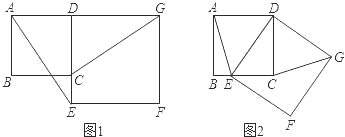
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
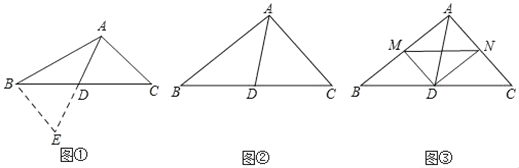
【题目】(问题情境)如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
(1)(问题解决)延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围是 .
(反思感悟)解题时,条件中若出现“中点”、“中线”字样,可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同个三角形中,从而解决问题.
(2)(尝试应用)如图②,△ABC中,∠BAC=90°,AD是BC边上的中线,试猜想线段AB,AC,AD之间的数量关系,并说明理由.
(3)(拓展延伸)如图③,△ABC中,∠BAC=90°,D是BC的中点,DM⊥DN,DM交AB于点M,DN交AC于点N,连接MN.当BM=4,MN=5,AC=6时,请直接写出中线AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com