
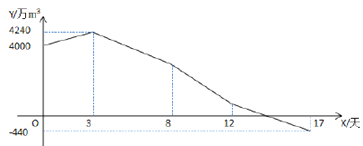
【题目】南方旱情严重,乙水库需每天向外供相同量的水. 3天后,为缓解旱情,北方甲水库立即以管道运输的方式给乙水库送水,在给乙水库送水前甲水库的蓄水量一直为5000万m3.由于两水库相距较远,甲水库的送出的水要5天后才能到达乙水库,12天后旱情缓解,乙水库不再向外供水,甲水库也停止向乙水库送水.下图是甲水库的蓄水量与乙水库蓄水量之差y(万m3)与时间x(天)之间的函数图象.则甲水库每天的送水量为__________万m3.(假设在单位时间内,甲水库的放水量与乙水库的进水量相同,水在排放、接收以及输送过程中的损耗不计).
【答案】300
【解析】
观察图象,根据一开始,甲水库的蓄水量与乙水库蓄水量之差,可以求出乙水库蓄水量,根据第3天时,甲水库的蓄水量与乙水库蓄水量之差,可以求出乙水库需每天向外供相同量,设甲水库每天的送水量为![]() 万m3,根据第17天时甲水库的蓄水量与乙水库蓄水量之差,列出方程,即可求解.
万m3,根据第17天时甲水库的蓄水量与乙水库蓄水量之差,列出方程,即可求解.
观察图象,根据一开始,甲水库的蓄水量与乙水库蓄水量之差为4000万m3,
则乙水库蓄水量为![]() 万m3,
万m3,
根据第3天时,甲水库的蓄水量与乙水库蓄水量之差为4240万m3,甲水库的蓄水量还为5000万m3
则乙水库蓄水量为![]() 万m3,
万m3,
乙水库每天向外供相水量为:![]() 万m3,
万m3,
设甲水库每天的送水量为![]() 万m3,根据第17天时甲水库的蓄水量与乙水库蓄水量之差为
万m3,根据第17天时甲水库的蓄水量与乙水库蓄水量之差为![]() ,
,
则![]()
解得:![]()
故答案为:300.


科目:初中数学 来源: 题型:
【题目】如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )
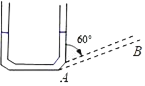
A. 4cmB. 2![]() cmC. 3cmD. 8cm
cmC. 3cmD. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
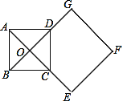
【题目】如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=![]() AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=__度时,∠OAG′=90°.
AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=__度时,∠OAG′=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若|m+3|+![]() =0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
=0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
A. y=![]() (x﹣3)2+2B. y=
(x﹣3)2+2B. y=![]() (x+3)2﹣2
(x+3)2﹣2
C. y=![]() (x﹣3)2﹣2D. y=
(x﹣3)2﹣2D. y=![]() (x+3)2+2
(x+3)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
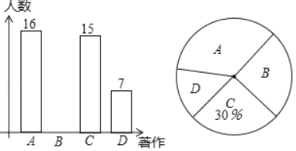
【题目】某校对A《唐诗》、B《宋词》、C《蒙山童韵》、D其它,这四类著作开展“最受欢迎的传统文化著作”调查,随机调查了若干名学生(每名学生必选且只能选这四类著作中的一种)并将得到的信息绘制了下面两幅不完整的统计图:
(1)求一共调查了多少名学生;
(2)请将条形统计图补充完整;
(3)该校语文老师想从这四类著作中随机选取两类作为学生寒假必读书籍,请用树状图或列表的方法求恰好选中《宋词》和《蒙山童韵》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
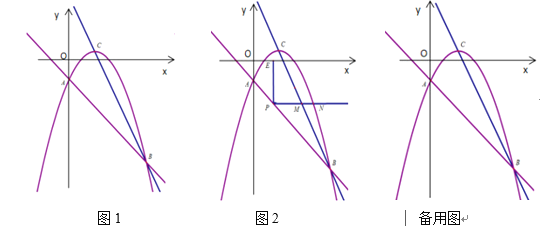
【题目】如图,直线![]() 与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为
与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为![]() .
.
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,射线![]() 轴并与直线BC和抛物线分别交于点M、N,过点P作
轴并与直线BC和抛物线分别交于点M、N,过点P作![]() 轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使
轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使![]() 的值最大,求
的值最大,求![]() 的最大值和此时Q的坐标;
的最大值和此时Q的坐标;
(3)在抛物线上找一点D,使△ABD为直角三角形,求D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块长和宽分别为40厘米和25厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体纸盒,使它的底面积为450平方厘米.那么纸盒的高是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
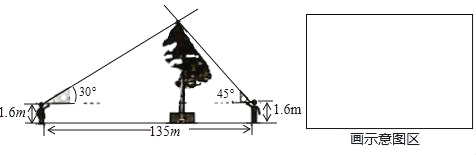
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.
(1)请在指定区域内画出小红和小阳测量古松树高的示意图;
(2)通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com