
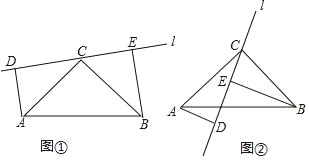
【题目】探究:如图①,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的同侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.求证:DE=AD+BE.
应用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的异侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.直接写出线段AD、BE、DE之间的相等关系.
【答案】探究:证明见解析;应用: AD=BE﹣DE,理由见解析.
【解析】
根据垂直得出∠ADC=∠ACB=∠BEC=90°,根据三角形的内角和定理和邻补角得出∠DAC=∠ECB,根据AAS证△ADC≌△CEB,推出AD=CE,DC=BE,代入即可.
①∵AD⊥DE,BE⊥DE,∠ACB=90°,∴∠ADC=∠ACB=∠BEC=90°,∴∠DAC+∠DCA=90°,∠DCA+∠ECB=180°﹣90°=90°,∴∠DAC=∠ECB.在△ADC和△CEB中,∵∠ADC=∠CEB,∠DAC=∠ECB,AC=BC,∴△ADC≌△CEB,∴AD=CE,DC=BE,∴DE=DC+CE=BE+AD,即DE=AD+BE.
②AD=BE﹣DE,理由如下:
∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°.
又∵∠ACB=90°,∴∠ACD=∠CBE=90°﹣∠ECB.
在△ACD与△CBE中,∵∠ADC=∠CEB,∠ACD=∠CBE,AC=BC,∴△ACD≌△CBE(AAS),∴CD=BE,AD=CE.
又∵CE=CD﹣DE,∴AD=BE﹣DE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
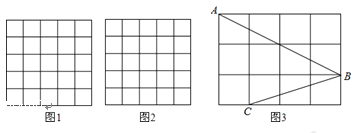
(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、 ![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、C、N三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,则∠BCM:∠BCN=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).
(1)当k=﹣2时,求反比例函数的解析式;
(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
(4)点C为x轴上一动点,且C点坐标为(2k,0),当△ABC是以AB为斜边的直角三角形时,求K的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先计算,再找出规律,然后根据规律进行计算.
(1)计算:①![]() ②
②![]() ③
③![]()
(2)根据(1)中的计算,用字母表示出你发现的规律.
![]() =__________________
=__________________
(3)根据(2)中的结论,计算下列结果:
①![]()
②![]()
③ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣20)+(+3)﹣(﹣5)
(2)(﹣5)×6×![]() ÷(﹣2)
÷(﹣2)
(3)﹣![]() ÷
÷![]() ﹣
﹣![]() ×(﹣9)
×(﹣9)
(4)(﹣1)4+5÷(﹣![]() )×(﹣6)
)×(﹣6)
(5)(![]() +
+![]() ﹣
﹣![]() )×36
)×36
(6)﹣1﹣[1![]() +(﹣12)÷6]×(﹣
+(﹣12)÷6]×(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直接写出计算结果:
(1) -2-11 = (2) 5-(-12)=
(3) (-5)×(-6) = (4) ![]()
(5)![]() = (6)
= (6) ![]() =
=
(7)-3.5+3.5 = (8)![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程:
计算:(-15)÷(![]() -1
-1![]() -3)×6.
-3)×6.
解:原式=(-15)÷(-![]() )×6(第一步)
)×6(第一步)
=(-15)÷(-25)(第二步)
=![]() .(第三步)
.(第三步)
解答:(1)上面解题过程,从第____步开始错误,错误的原因是_____.
(2)请写出正确的解题过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com