
| 1�� | 2�� | 3�� | 4�� | 5�� | �ܷ� | |
| �װ� | 100 | 98 | 110 | 89 | 103 | 500 |
| �Ұ� | 86 | 100 | 98 | 119 | 97 | 500 |
| ������ | ��� | ���� | |
| �װ� | 60% | 100 | 46.8 |
| �Ұ� | 40% | 98 | 114 |
���� ��1�����ݸ�����������������ʣ�������λ���ĸ���ͷ��ʽ���㼴�ɣ�
��2��������λ�������ʺͷ�������ʽ�ɣ�
��� �⣺��1���װ��������Ϊ��3��5��100%=60%��
�Ұ��������Ϊ��2��5��100%=40%��
�װ����λ��Ϊ100���Ұ����λ��Ϊ98��
�װ��ƽ����Ϊ100���Ұ��ƽ����Ϊ100��
�װ�ķ���Ϊ��$\frac{1}{5}$[��100-100��2+��98-100��2+��110-100��2+��89-100��2+��103-100��2]=46.8��
�Ұ�ķ���Ϊ��$\frac{1}{5}$[��86-100��2+��100-100��2+��98-100��2+��119-100��2+��97-100��2]=114��
��2����Ϊ�װ�������ʱȽϸߡ���λ������С���Ƚ��ȶ���
����Ӧ�ðѹھ���״�����Ӱ࣮
���� ���⿼����Ƿ���ļ��㡢��λ����ȷ����ƽ�����ļ��㣬���շ���ļ��㹫ʽ��S2=$\frac{1}{n}$[��x1-x��2+��x2-x��2+��+��xn-x��2]������$\overline{x}$Ϊn������x1��x2������xn��ƽ�����ǽ���Ĺؼ���


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
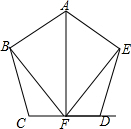 ��ͼ����F��CD ���е㣬��AF��CD��BC=ED����BCD=��EDC��
��ͼ����F��CD ���е㣬��AF��CD��BC=ED����BCD=��EDC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���������������У���A��B��C��M��N���ڸ���ϣ�
��ͼ���������������У���A��B��C��M��N���ڸ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
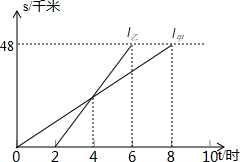 �ס������˵��������Σ��������г�������綯��������ͬ·��ǰ������ͼ��l����l���ֱ��ʾ�ס���ǰ��Ŀ�ĵ����ߵ�·��s/ǧ�������õ�ʱ��t/ʱ�Ĺ�ϵ��
�ס������˵��������Σ��������г�������綯��������ͬ·��ǰ������ͼ��l����l���ֱ��ʾ�ס���ǰ��Ŀ�ĵ����ߵ�·��s/ǧ�������õ�ʱ��t/ʱ�Ĺ�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ⲻ��ʽ��$\left\{\begin{array}{l}{x+3��5��}\\{2x+1��3��2-x����}\end{array}\right.$��
�ⲻ��ʽ��$\left\{\begin{array}{l}{x+3��5��}\\{2x+1��3��2-x����}\end{array}\right.$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com