
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ������Ϊ ![]() �ĵ���ֱ�����ǰ�ABC���ڵڶ����ޣ���б�������������ϣ�ֱ�Ƕ���C������Ϊ����1��0������B��������y=ax2+ax��2�ϣ�
�ĵ���ֱ�����ǰ�ABC���ڵڶ����ޣ���б�������������ϣ�ֱ�Ƕ���C������Ϊ����1��0������B��������y=ax2+ax��2�ϣ�
��1����A������Ϊ �� ��B������Ϊ��
��2�������ߵĽ���ʽΪ��
��3���裨2���������ߵĶ���ΪD�����DBC�������
��4�������������Ƿ��ڵ�P����B���⣩��ʹ��ACP��Ȼ����ACΪֱ�DZߵĵ���ֱ�������Σ������ڣ���ֱ��д�����е�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1����0��2��������3��1��
��2��y= ![]() x2+
x2+ ![]() x��2
x��2
��3��
�⣺�ɣ�2���������ߵĽ���ʽ��֪�������ߵĶ���D���� ![]() ����
���� ![]() ����
����
��ֱ��BD�Ĺ�ϵʽΪy=kx+b������B��D���������ã�
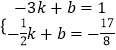 ��
��
��� 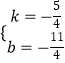 ��
��
��BD�Ĺ�ϵʽΪy=�� ![]() x��
x�� ![]() ��
��
��ֱ��BD��x �ύ��ΪE�����E���� ![]() ��0����CE=
��0����CE= ![]() ��
��
��S��DBC= ![]() ��
�� ![]() ����1+
����1+ ![]() ��=
��= ![]()
��4��
�⣺������ڵ�P��ʹ�á�ACP��Ȼ����ACΪֱ�DZߵĵ���ֱ�������Σ�
�����Ե�CΪֱ�Ƕ��㣻
���ӳ�BC����P1��ʹ��P1C=BC���õ�����ֱ�������Ρ�ACP1��
����P1��P1M��x�ᣬ
��CP1=BC����MCP1=��BCF����P1MC=��BFC=90�㣬
���MP1C�ա�FBC��
��CM=CF=2��P1M=BF=1��
��P1��1����1����
�����Ե�AΪֱ�Ƕ��㣻
i�������A��AP2��CA����ʹ��AP2=AC���õ�����ֱ�������Ρ�ACP2��
����P2��P2N��y�ᣬͬ����֤��AP2N�ա�CAO��
��NP2=OA=2��AN=OC=1��
��P2��2��1����
ii�����Ե�PΪֱ�Ƕ��㣮
��P3��P3G��y����G��
ͬ������AGP3�ա�CAO��
��GP3=OA=2��AG=OC=1��
��P3����2��3����
�����飬��P1��1����1�����P2��2��1������������y= ![]() x2+
x2+ ![]() x��2�ϣ���P3����2��3�������������ϣ�
x��2�ϣ���P3����2��3�������������ϣ�
�ʵ�P������ΪP1��1����1����P2��2��1����
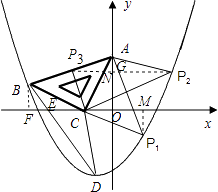
���������⣺��1����C����1��0����AC= ![]() ��
��
��OA= ![]() =
= ![]() =2��
=2��
��A��0��2����
����B��BF��x�ᣬ����ΪF��
�ߡ�ACO+��CAO=90�㣬��ACO+��BCF=90�㣬��BCF+��FBC=90�㣬
�ڡ�AOC���CFB�У�
�� 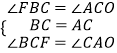 ��
��
���AOC�ա�CFB��
��CF=OA=2��BF=OC=1��
��OF=3��
��B����������3��1����
���Դ��ǣ���0��2��������3��1������2���߰�B����3��1������y=ax2+ax��2�ã�
1=9a��3a��2��
���a= ![]() ��
��
�������߽���ʽΪ��y= ![]() x2+
x2+ ![]() x��2��
x��2��
���Դ��ǣ�y= ![]() x2+
x2+ ![]() x��2��
x��2��
�����㾫����������Ҫ�����˵���ֱ�������κͶ��κ�����ͼ������֪ʶ�㣬��Ҫ���յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ���ͼ��ƴ��һ���µ�ͼ�Σ���ͨ��ͼ������ļ��㣬�������Եõ�һЩ���õ���Ϣ����������һЩ������ͼ�ε����.
(1)��ͼ1��ʾ����һ�ų�����ֽ�尴ͼ�����߲ü��ɾſ飬�����������DZ߳���Ϊm�Ĵ������Σ������DZ߳���Ϊn��С�����Σ�����dz�Ϊm����Ϊn��ȫ��С�����Σ���m>n.�۲�ͼ�Σ����Է��ִ���ʽ2m2��5mn��2n2������ʽ�ֽ�Ϊ .
(2)��ͼ1��ÿ��С�����ε����Ϊ12cm2���ĸ������ε������Ϊ50 cm2������ͼ�����вü���(���߲���)��֮��.
(3)��ͼ2�б߳�Ϊa��b��������ƴ��һ��B,C,G������ͬһ��ֱ���ϣ�����BD��BF���������������εı߳�����a+b=10��ab=16���������Ӱ���ֵ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ����( )

A. ��AC��BC���߸��ߵĽ��㴦
B. ��AC��BC�������ߵĽ��㴦
C. ��AC��BC���ߴ�ֱƽ���ߵĽ��㴦
D. ����A����B���ڽ�ƽ���ߵĽ��㴦
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ת��������ѧ�е�һ����Ҫ˼�룬����İ��������ת������Ϥ�����⣬�Ѹ��ӵ�����ת���ɼ����⣬�ѳ��������ת��Ϊ��������⣮
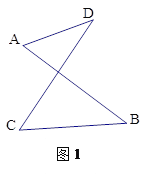
��֪����ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8���Ρ����Խ���������⣺
����һ����ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ�� ����
���������ͼ2�У�����D=40�㣬��B=36�㣬��DAB����BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N��������P�Ķ�����
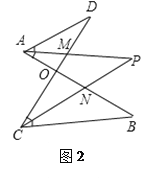
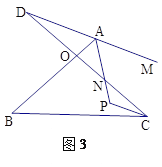
����������ͼ3�У���֪AP��CP�ֱ�ƽ�֡�BAM����BCD��������P����B����D֮�������������������ϵ����˵�����ɣ�
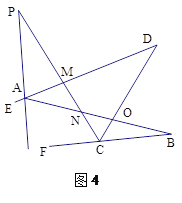
�����ģ���ͼ4�У���֪AP�ķ����ӳ���ƽ�֡�EAB��CPƽ�֡�DCF����ֱ��д����P����B����D֮���������ϵ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ3����ABC�ڽ��ڡ�O��AB=3 ![]() ��AC=3
��AC=3 ![]() ��D�ǡ�O��һ�㣬��AD=3����CD�ij�Ӧ�ǣ� ��
��D�ǡ�O��һ�㣬��AD=3����CD�ij�Ӧ�ǣ� ��
A.3
B.6
C.![]()
D.3��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A�������ǣ�4��3������ԲD����A��O���ֱ�����������������ύ�ڵ�E��F����EF��OAʱ����ʱEF= �� 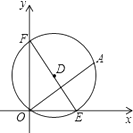
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ֵ��ӻ�ԭ��ÿ̨2600Ԫ�������ڼ��Ծ����۳��ۣ������̼ҹ涨��2000Ԫ��200Ԫ�����������ֵ��ӻ�ʵ����Ҫ����Ǯ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪l1��l2��MN�ֱ��ֱ��l1��l2���ڵ�A��B��ME�ֱ��ֱ��l1��l2���ڵ�C��D����P��MN�ϣ�P����A��B��M���㲻�غϣ���
��1�������P��A��B����֮���˶�ʱ�����������¡�����֮���к�������ϵ��˵�����ɣ�
��2�������P��A��B��������˶�ʱ�����������¡������к�������ϵ��ֻ��д�����ۣ���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com