
【题目】如图,![]() 平分
平分![]() ,且
,且![]() ,垂足分别是
,垂足分别是![]() ,连结
,连结![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() 是线段
是线段![]() 的垂直平分线;
的垂直平分线;
(2)若![]() ,求
,求![]() 的周长和四边形
的周长和四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() ,
,![]()
【解析】
(1)根据线段垂直平分线的判定定理证明点E,点O都在线段CD的垂直平分线上,即可得到![]() 是线段
是线段![]() 的垂直平分线;
的垂直平分线;
(2)先证明△OCD是等边三角形,再根据等边三角形的性质即可得出周长及面积.
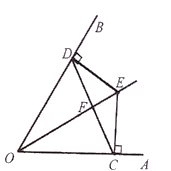
(1)证明:∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴CE=DE,
∴点E是在线段CD的垂直平分线上.
在Rt△OCE和Rt△ODE中,
![]() ,
,
∴Rt△OCE≌Rt△ODE(HL),
∴OC=OD,
∴点O是在线段CD的垂直平分线上,
∴OE是线段CD的垂直平分线.
(2)解:∵∠ECD=30°,∠OCE=90°,
∴∠OCD=60°.
∵OC=OD,
∴△OCD是等边三角形.
∵OC=![]() ,
,
∴△OCD的周长为3![]()
∵∠OCD=60°,
∴∠COE=30°,
∴OE=2CE.
设CE=x,则OE=2x.
由勾股定理,得(2x)2=x2+(![]() )2,
)2,
解得:x=1,即CE=1,
∴四边形OCED的面积=2S△OCE=2×![]() ·OC·EC=
·OC·EC=![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
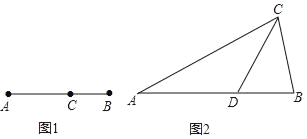
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们已经学过:点C将线段AB分成两部分,如果![]() ,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
如图2,在△ABC中,∠A=36°,AB=AC,∠C的平分线交AB于点D.
(1)证明点D是AB边上的黄金分割点;
(2)证明直线CD是△ABC的黄金分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)当一次函数的函数值大于反比例函数的函数值时,直接写出自变量x的取值范围为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 两种机器人都被用来搬运化工原料,
两种机器人都被用来搬运化工原料,![]() 型机器人每小时搬运的化工原料是
型机器人每小时搬运的化工原料是![]() 型机器人每小时搬运的化工原料的1.5倍,
型机器人每小时搬运的化工原料的1.5倍,![]() 型机器人搬运900
型机器人搬运900![]() 所用时间比
所用时间比![]() 型机器人搬运800
型机器人搬运800![]() 所用时间少1小时.
所用时间少1小时.
(1)求两种机器人每小时分别搬运多少化工原料?
(2)某化工厂有8000![]() 化工原料需要搬运,要求搬运所有化工原料的时间不超过5小时,现计划先由6个
化工原料需要搬运,要求搬运所有化工原料的时间不超过5小时,现计划先由6个![]() 型机器人搬运3小时,再增加若干个
型机器人搬运3小时,再增加若干个![]() 型机器人一起搬运,请问至少要增加多少个
型机器人一起搬运,请问至少要增加多少个![]() 型机器人?
型机器人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接祖国七十周年庆典,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运16趟可完成,需支付运费5400元.已知甲、乙两车单独运完此垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟;
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人承包了一池塘养鱼,他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼,把每条鱼都作上标记,放回鱼塘;过了2天,他让他父亲从鱼塘内打捞上了50条鱼,结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤,平均每条鱼估计2.3斤,你能帮助他估计一下今年的收入情况吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com