
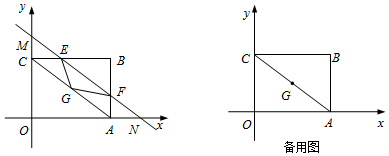
���� ��1���߸��ݹ��ɶ����õ�AC=$\sqrt{42+32}$=5��CE=1��ͼ1������CF���������������ε����ʼ��ɵõ����ۣ�
��2����0��t��3ʱ���ѡ�EFG���ߵ�ƽ����ʾ��������EFG��ֱ�������������ֿ��ܣ��г��������̣��ֱ������ɣ�ͬ����3��t��6ʱ���ѡ�EFG���ߵ�ƽ����ʾ��������EFG��ֱ��������Ҳ�����ֿ��ܣ�ͬ�����t��ֵ��
��3��GG�����ڵ�ֱ����ֱ��CA��ֱ���ҹ�G�㣬�ʱ���ʽΪy=$\frac{4}{3}$x-$\frac{7}{6}$���ֱ����ֱ��GG����ֱ��CB��BA��OA��OC�Ľ���G����е���ֱ��MN�ϼ��ɵõ���������Ĵ𰸣�
��� 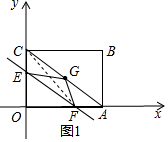 �⣺��1����A��4��0����C��0��3��
�⣺��1����A��4��0����C��0��3��
��OA=4��OC=3��
��AC=$\sqrt{42+32}$=5��CE=1
��ͼ1������CF��
��EF��AC��
���OEF�ס�OCA��
��$\frac{OE}{OC}$=$\frac{OF}{OA}$��
��$\frac{2}{3}$=$\frac{OF}{4}$��
��OF=$\frac{8}{3}$��
��S=S��CEF=$\frac{1}{2}$��1��$\frac{8}{3}$=$\frac{4}{3}$��
��2���ٵ�0��t��3ʱ��E��0��t����F��$\frac{4}{3}$t��0����G��2��$\frac{3}{2}$����
��EF2=$\frac{25}{9}$t2��EG2=22+��t-$\frac{3}{2}$��2��GF2=��$\frac{4}{3}$t-2��2+��$\frac{3}{2}$��2��
��EF2+EG2=GF2������$\frac{25}{9}$t2+22+��t-$\frac{3}{2}$��2=��$\frac{4}{3}$t-2��2+��$\frac{3}{2}$��2�����t=0����ȥ����t=-$\frac{7}{3}$����ȥ����
��EF2+FG2=EG2������$\frac{25}{9}$t2+��$\frac{4}{3}$t-2��2+��$\frac{3}{2}$��2=22+��t-$\frac{3}{2}$��2�����t=0����ȥ����t=$\frac{21}{32}$��
��EG2+GF2=EF2������22+��t-$\frac{3}{2}$��2+��$\frac{4}{3}$t-2��2+��$\frac{3}{2}$��2=$\frac{25}{9}$t2�����t=$\frac{3}{2}$��
�ڵ�3��t��6ʱ��E��$\frac{4}{3}$t-4��3����F��4��t-3����G��2��$\frac{3}{2}$����
��EF2=��$\frac{4}{3}$t-8��2+��t-6��2��EG2=��$\frac{4}{3}$t-6��2+��$\frac{3}{2}$��2��GF2=22+��t-$\frac{9}{2}$��2��
��EF2+EG2=GF2�����У�$\frac{4}{3}$t-8��2+��t-6��2+��$\frac{4}{3}$t-6��2+��$\frac{3}{2}$��2=22+��t-$\frac{9}{2}$��2��������32t2-363t+1026=0����=441�����t=$\frac{171}{32}$��t=6����ȥ����
��EF2+FG2=EG2�����У�$\frac{4}{3}$t-8��2+��t-6��2+22+��t-$\frac{9}{2}$��2=��$\frac{4}{3}$t-6��2+��$\frac{3}{2}$��2��������6t2-79t+258=0����=49�����t=6����ȥ����t=$\frac{43}{6}$��6����ȥ����
��EG2+GF2=EF2������$\frac{4}{3}$t-6��2+��$\frac{3}{2}$��2+22+��t-$\frac{9}{2}$��2=��$\frac{4}{3}$t-8��2+��t-6��2�����t=$\frac{9}{2}$��
���Ͽ�֪����EFGΪֱ��������ʱ��t=$\frac{21}{32}$��t=$\frac{3}{2}$��t=$\frac{9}{2}$��t=$\frac{171}{32}$��
��3��ֱ��MNΪy=-$\frac{3}{4}$x+t��G��2��$\frac{3}{2}$����
GG�����ڵ�ֱ����ֱ��CA��ֱ���ҹ�G�㣬�ʱ���ʽΪy=$\frac{4}{3}$x-$\frac{7}{6}$����y=$\frac{4}{3}$x-$\frac{7}{6}$�У�
��x=0���ɵã�y=-$\frac{7}{6}$����G�䣨0��-$\frac{7}{6}$����GG���е㣨1��$\frac{1}{6}$��������ֱ��MNΪy=-$\frac{3}{4}$x+t�����t=$\frac{11}{12}$��
��y=0���ɵã�x=$\frac{7}{8}$����G�䣨$\frac{7}{8}$��0����GG���е㣨$\frac{23}{16}$��$\frac{3}{4}$��������ֱ��MNΪy=-$\frac{3}{4}$x+t�����t=$\frac{117}{64}$��
��x=4���ɵã�y=$\frac{25}{6}$����G�䣨4��$\frac{25}{6}$����GG���е㣨3��$\frac{17}{6}$��������ֱ��MNΪy=-$\frac{3}{4}$x+t�����t=$\frac{61}{12}$��
��y=3���ɵã�x=$\frac{25}{8}$����G�䣨$\frac{25}{8}$��3����GG���е㣨$\frac{41}{16}$��$\frac{9}{4}$��������ֱ��MNΪy=-$\frac{3}{4}$x+t�����t=$\frac{267}{64}$��
���Ͽ�֪����������t��ֵΪ$\frac{11}{12}$��$\frac{117}{64}$��$\frac{61}{12}$��$\frac{267}{64}$��
���� ������Ҫ����һ�κ�������ʽ�����������ε��ж������ʡ����ɶ�����һԪ���η��̵��ۺ�Ӧ�ã��ڣ�1�����ֱܷ���t��ʾ����EFG�еĵ��ǽ���Ĺؼ����ڣ�2����ע���������ۣ��ڣ�3�����������ó�GG�����ڵ�ֱ����ֱ��CA��ֱ���ҹ�G�㣬�ǽ���Ĺؼ�������������Ƚϴ�������϶࣬����©������һ�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
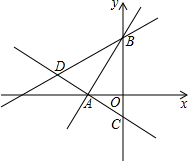 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�����A��-$\sqrt{3}$��0��������ֱ�߷ֱ�y����B��C���㣬��ABO=30�㣬OB=3OC��
��ͼ��ʾ����ƽ��ֱ������ϵ�У�����A��-$\sqrt{3}$��0��������ֱ�߷ֱ�y����B��C���㣬��ABO=30�㣬OB=3OC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 35��104 | B�� | 350��103 | C�� | 3.5��105 | D�� | 0.35��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com