
如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,现将△ABC沿射线BC的方向平移![]() (
(![]() <5)个单位得到△DEF.
<5)个单位得到△DEF.
(1)(4分)求EF的长度;
(2)(4分)当![]() =3时,连接AE、BD,试判断AE、BD之间的位置关系,并说明理由;
=3时,连接AE、BD,试判断AE、BD之间的位置关系,并说明理由;
 (3)(5分)探究:当
(3)(5分)探究:当![]() 为何值时,△ADE是等腰三角形.
为何值时,△ADE是等腰三角形.
解:
(1)在Rt△ABC中,∠BAC=90°,
∴![]() , … 2分
, … 2分
∴![]() . …………………………… 4分
. …………………………… 4分
 (2)AE、BD之间的
(2)AE、BD之间的![]() 位置关系是垂直且平分. … 5分
位置关系是垂直且平分. … 5分
理由是:
连结AD.
∵AB∥DE,AD∥BE,
∴四边形ABED是平行四边形,…………… 6分
又∵AB=BE=3,
∴四边形ABED是菱形,…………………… 7分
∴AE、BD垂直且平分. …………………… 8分
(3)分三种情况讨论:
①当![]() 时,△ADE是等腰三角形;…… 9分
时,△ADE是等腰三角形;…… 9分
②当![]() 时,△ADE是等腰三角形.
时,△ADE是等腰三角形.
 作
作![]() ,垂足为M,则有:
,垂足为M,则有:
![]() ,
,
在Rt△AEM中,由勾股定理得:
![]() ,
,
即:![]() ,
,
解得![]() . ……………………………………… 10分
. ……………………………………… 10分
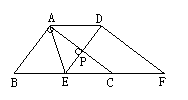 ③方法一:
③方法一:
当![]() 时,△ADE是等腰三角形.
时,△ADE是等腰三角形.
∵当![]() 时,
时,![]() ,
,
∵∠BAC=90°,
∴![]() , …………………………………………………………… 11分
, …………………………………………………………… 11分
又∵![]()
∴![]() , ……………………………………………………………… 12分
, ……………………………………………………………… 12分
即当![]() 时,△ADE是等腰三角形;
时,△ADE是等腰三角形;
综上所述,当![]() 或
或![]() 或
或![]() 时,△ADE是等腰三角形. ………………… 13分
时,△ADE是等腰三角形. ………………… 13分
方法二:
当AE=AD时,△ADE是等腰三角形.
 设Rt△ABC中BC边上的高为
设Rt△ABC中BC边上的高为![]() ,则有:
,则有:![]() ,解得
,解得![]() .
.
由已知可得:![]() ,设垂足为点P,
,设垂足为点P,
∵AE=DE,
∴![]() ,
,
∵![]() ,
,
即:![]() ,解得
,解得![]() , …………………………………………… 11分
, …………………………………………… 11分
在Rt△AEP中,∠APE=90°,
∴![]() ,即:
,即:![]() ,解得:
,解得:![]() ,……… 12分
,……… 12分
即当![]() 时,△ADE是等腰三角形;
时,△ADE是等腰三角形;
综上所述,当![]() 或
或![]() 或
或![]() 时,△ADE是等腰三角形. …………………… 13分
时,△ADE是等腰三角形. …………………… 13分


科目:初中数学 来源: 题型:
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
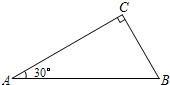 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
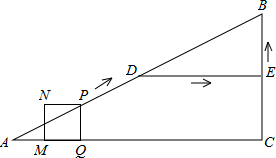 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com