
分析 根据三角形的中位线平行于第三边,且等于第三边的一半.需注意新四边形的形状只与对角线有关,不用考虑原四边形的形状依次填空即可.
解答 解:(1)顺次连接任意一个四边形的四边中点,所得四边形是平行四边形.理由如下:
如图,已知任意四边形ABCD,E、F、G、H分别是各边中点.连接BD.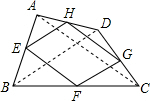
∵在△ABD中,E、H是AB、AD中点,
∴EH∥BD,EH=$\frac{1}{2}$BD.
∵在△BCD中,G、F是DC、BC中点,
∴GF∥BD,GF=$\frac{1}{2}$BD,
∴EH=GF,EH∥DF,
∴四边形EFGH为平行四边形.
(2)顺次连接任意一个对角线相等的四边形各边中点得出的四边形是矩形.理由如下: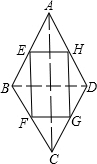
∵E,F是中点,
∴EH∥BD,
同理,EF∥AC,GH∥AC,FG∥BD,
∴EH∥FG,EF∥GH,
则四边形EFGH是平行四边形.
又∵AC⊥BD,
∴EF⊥EH,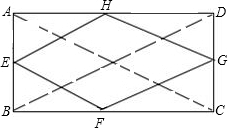
∴平行四边形EFGH是矩形.
(3)顺次连接任意对角线互相垂直的四边形各边中点所得四边形是菱形.理由如下:
如图,连接AC、BD.
在△ABD中,
∵AH=HD,AE=EB,
∴EH=$\frac{1}{2}$BD,
同理FG=$\frac{1}{2}$BD,HG=$\frac{1}{2}$AC,EF=$\frac{1}{2}$AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.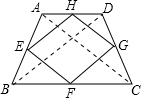 (4)顺次连接任意一个对角线相等且互相垂直的四边中点,所得四边形是正方形.理由如下:
(4)顺次连接任意一个对角线相等且互相垂直的四边中点,所得四边形是正方形.理由如下:
连接AC、BD.
∵E、F、G、H分别是AB、BC、CD、DA的中点
∴EF=$\frac{1}{2}$AC,GH=$\frac{1}{2}$AC,EH=$\frac{1}{2}$BD,GF=$\frac{1}{2}$BD
∵AB=CD,
∴AC=BD,
∴EF=GH=EH=GF,
∴四边形EFGH菱形,
∵∠HEF=90°,
∴四边形EFGH正方形,
故答案为:任意,对角线互相垂直,对角线相等,对角线相等且互相垂直.
点评 本题主要考查了三角形的中位线的性质,平行四边形的判定、矩形的判定定理、正方形的判定定理,难度适中,解题的关键是熟记三角形中位线定义以及各种特殊四边形的判定方法.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
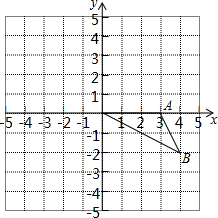 如图,在边长为1的网格中建立平面直角坐标系xOy,O、A、B三点均为格点.
如图,在边长为1的网格中建立平面直角坐标系xOy,O、A、B三点均为格点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
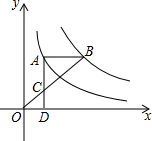 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )| A. | 2015 | B. | 2016 | C. | $\sqrt{2015}$ | D. | $\sqrt{2016}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.| A. | 1 | B. | 1或3 | C. | 1或7 | D. | 3或7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com