
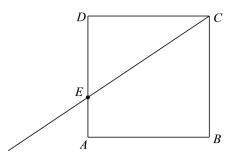
【题目】已知:如图,在正方形ABCD中,点E在AD边上运动,从点A出发向点D运动,到达D点停止运动.作射线CE,并将射线CE绕着点C逆时针旋转45°,旋转后的射线与AB边交于点F,连接EF
(1)依题意补全图形;
(2)猜想线段DE,EF,BF的数量关系并证明;
(3)过点C作CG⊥EF,垂足为点G,若正方形ABCD的边长是4,请直接写出点G运动的路线长.
【答案】(1)见解析;(2)EF=DE+BF,见解析;(3)2π
【解析】
(1)依题意补全图形即可;
(2)延长AD到点H,使DH=BF,连接CH,证明△CDH≌△CBF(SAS).得出CH=CF,∠DCH=∠BCF.证明△ECH≌△ECF(SAS).得出EH=EF.即可得出结论;
(3)确定点G的运动轨迹,利用弧长公式计算即可.
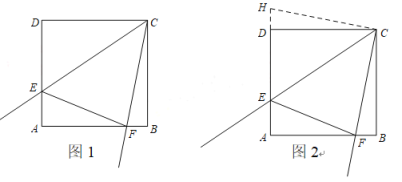
解:(1)补全图形如图1.
(2)线段DE,EF,BF的数量关系是 EF=DE+BF
证明:延长AD到点H,使DH=BF,连接CH(如图2).
易证△CDH≌△CBF.
∴CH= CF,∠DCH=∠BCF.
∵∠ECF=45°,
∴∠ECH=∠ECD+∠DCH= ∠ECD +∠BCF =45°.
∴∠ECH=∠ECF=45°.
又∵CE= CE,
∴△ECH≌△ECF.
∴EH= EF.
∴EF=DE+BF.
(3)点G运动的路线长为2π


科目:初中数学 来源: 题型:
【题目】哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?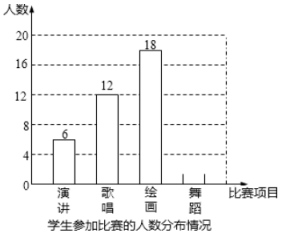
查看答案和解析>>
科目:初中数学 来源: 题型:
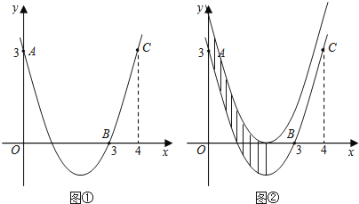
【题目】如图①,已知抛物线![]() 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛,该校七、八年级各有学生![]() 人,各随机抽取
人,各随机抽取![]() 名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
![]()
八年级:
![]()
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]() ,
,![]() ,
,![]() _
_
![]() 该校对读书知识竞赛成绩不少于
该校对读书知识竞赛成绩不少于![]() 分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
![]() 结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点,(不与B、C重合)在AC边上取一点E,使∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y.
①求y关于x的函数关系式并写出自变量x的取值范围;
②求y的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
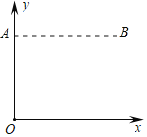
【题目】某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间(不包括A、B两点)经过时,将触发报警.现将A、B两点放置于平面直角坐标系![]() 中,(如图),已知点A、B的坐标分别为(0,4),(4,4),小车沿抛物线
中,(如图),已知点A、B的坐标分别为(0,4),(4,4),小车沿抛物线![]() (
(![]() <0)运动.若小车在运动过程中触发两次报警装置,则
<0)运动.若小车在运动过程中触发两次报警装置,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球和足球.已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.
(1)每个篮球、每个足球的价格分别为多少元?
(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com