
【题目】如图,抛物线y=ax2+bx+c经过点A(0,﹣3)、B(﹣1,0)、C(2,﹣3),抛物线与x轴的另一交点为点E,点P为抛物线上一动点,设点P的横坐标为t.
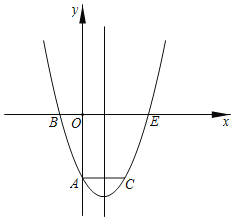
(1)求抛物线的解析式;
(2)若点P在第一象限,点M为抛物线对称轴上一点,当四边形MBEP恰好是平行四边形时,求点P的坐标;
(3)若点P在第四象限,连结PA、PE及AE,当t为何值时,△PAE的面积最大?最大面积是多少?
(4)是否存在点P,使△PAE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)P(4,5);(3)当t=![]() 时,S有最大值
时,S有最大值![]() ;(4)存在,理由,点P的坐标为:(﹣2,5)或(1,﹣4)
;(4)存在,理由,点P的坐标为:(﹣2,5)或(1,﹣4)
【解析】
(1)抛物线y=ax2+bx+c经过点A(0,﹣3)、C(2,﹣3),则函数的对称轴为:x=1,故点E(3,0),即可求解;
(2)四边形MBEP恰好是平行四边形时,则MP=BE=3,故t=4,则点P(4,5);
(3)△PAE的面积S=![]() PH×OE=
PH×OE=![]() (t﹣3﹣t2+2t+3)=
(t﹣3﹣t2+2t+3)=![]() (﹣t2+3t),即可求解;
(﹣t2+3t),即可求解;
(4)分∠PEA=90°、∠PAE=90°两种情况,分别求解即可.
解:(1)抛物线y=ax2+bx+c经过点A(0,﹣3)、C(2,﹣3),则函数的对称轴为:x=1,
故点E(3,0),
抛物线表达式为:y=a(x﹣3)(x+1)=a(x2﹣2x﹣3),
故﹣3a=﹣3,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3…①;
(2)四边形MBEP恰好是平行四边形时,则MP=BE=4,
故t=4,则点P(4,5);
(3)过点C作y轴的平行线交AE于点H,
由点A、E的坐标得直线AE的表达式为:y=x﹣3,

设点P(t,t2﹣2t﹣3),则点H(t,t﹣3),
△PAE的面积S=![]() PH×OE=
PH×OE=![]() (t﹣3﹣t2+2t+3)=
(t﹣3﹣t2+2t+3)=![]() (﹣t2+3t),
(﹣t2+3t),
当t=![]() 时,S有最大值
时,S有最大值![]() ;
;
(4)直线AE表达式中的k值为1,则与之垂直的直线表达式中的k为﹣1.
①当∠PEA=90°时,
直线PE的表达式为:y=﹣x+b,经点E的坐标代入并解得:
直线PE的表达式为:y=﹣x+3…②,
联立①②并解得:x=﹣2或3(舍去3),
故点P(﹣2,5);
②当∠PAE=90°时,
同理可得:点P(1,﹣4);
综上,点P的坐标为:(﹣2,5)或(1,﹣4).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
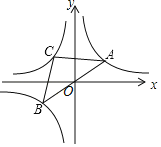
【题目】如图,已知A,B为反比例函数y1=![]() 图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=
图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=![]() (k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且
(k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且![]() 时,k的值为( )
时,k的值为( )
A.﹣![]() B.﹣3C.﹣4D.﹣
B.﹣3C.﹣4D.﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除,如果差太大或心算不易看出是否7的倍数,就需要继续上述[截尾、倍大、相减、验差]的过程,直到能清楚判断为止.
例如,判断126是否7的倍数的过程如下:
12﹣6×2=0,0是7的倍数,所以126是7的倍数;
又例如判断6789是否7的倍数的过程如下:
678﹣9×2=660,66﹣0×2=66,66不是7的倍数,所以6789不是7的倍数.
(1)请判断2019和2555是否能被7整除,并说明理由;
(2)有一个千位数字是1的四位正整数,百位数字与十位数字的和是7,个位数字是十位数字的3倍,且这个四位正整数是7的倍数,求这个四位正整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
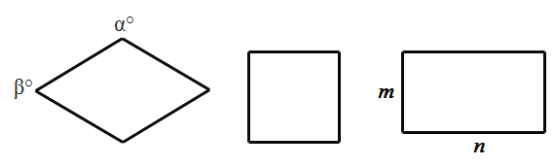
【题目】如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为![]() ,
,![]() ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为![]() ,于是
,于是![]() 越小,菱形越接近正方形.
越小,菱形越接近正方形.
①若菱形的一个内角为![]() ,则该菱形的“接近度”为_________;
,则该菱形的“接近度”为_________;
②当菱形的“接近度”等于_________时,菱形是正方形;
(2)设矩形的长和宽分别为![]() ,
,![]()
![]() ,试写出矩形的“接近度”的合理定义.
,试写出矩形的“接近度”的合理定义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3)、B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
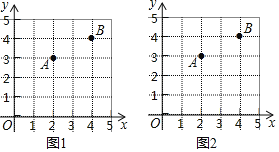
(1)在图1中画一个△QAB,使点Q的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P、B横坐标的平方和等于它们纵坐标和的4倍;
(3)在图2中的线段AB上确定点N,连结线段PN,使S△PAN=S△PBN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量![]() 取
取![]() 时,函数值
时,函数值![]() 也等于
也等于![]() ,则称
,则称![]() 是这个函数的不动点.
是这个函数的不动点.
已知二次函数![]() .
.
(1)若3是此函数的不动点,则![]() 的值为__________.
的值为__________.
(2)若此函数有两个相异的不动点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
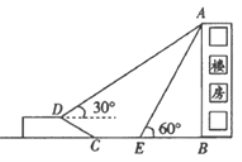
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为300 ,沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为600 .已知坡面CD=10米,山坡的坡度![]() (坡度 是指坡面的铅直高度与水平宽度的比),
(坡度 是指坡面的铅直高度与水平宽度的比),
(1)求点D离地面高度(即点D到直线BC的距离);
(2)求楼房AB高度.(结果保留根式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在七年级、八年级开展了阅读文学名著知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(单位:分),并对数据进行整理、描述和分析.下面给出了部分信息.
a.七年级学生知识竞赛成绩的平均数、中位数、众数、优秀率(80分及以上)如下表所示:
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 84. 2 | 77 | 74 | 45﹪ |
b.八年级学生知识竞赛成绩的扇形统计图如下(数据分为5组,A:50≤x≤59; B:60≤x≤69;C:70≤x≤79;D:80≤x≤89;E:90≤x≤100)
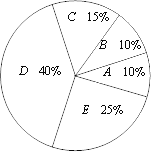
c.八年级学生知识竞赛成绩在D组的是:87 88 88 88 89 89 89 89
根据以上信息,回答下列问题:
(1)八年级学生知识竞赛成绩的中位数是 分;
(2)请你估计该校七、八年级所有学生中达到“优秀”的有多少人?
(3)下列结论:①八年级成绩的众数是89分;②八年级成绩的平均数可能为86分;③八年级成绩的极差可能为50分.其中所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若P和Q两点关于原点对称,则称点P与点Q是一个“和谐点对”,表示为[P,Q],比如[P(1,2),Q(﹣1,﹣2)]是一个“和谐点对”.
(1)写出反比例函数y=![]() 图象上的一个“和谐点对”;
图象上的一个“和谐点对”;
(2)已知二次函数y=x2+mx+n,
①若此函数图象上存在一个和谐点对[A,B],其中点A的坐标为(2,4),求m,n的值;
②在①的条件下,在y轴上取一点M(0,b),当∠AMB为锐角时,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com