
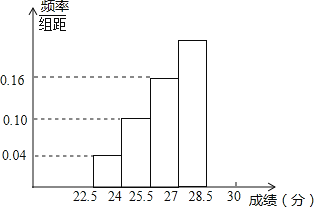
【题目】某区为了了解九年级学生身体素质情况,从中随机抽取了部分学生进行测试,测试成绩的最高分为30分,最低分为23分,按成绩由低到高分成五组(每组教据可含最大值,不含最小值),绘制的频率分布直方图中缺少了28.5分~30分的一组(如图所示),已知27分~28.5分一组的频率为0.31,且这组学生人数比25.5分~27分这组学生多了28人,根据图示及上述相关信息解答下列问题:
(1)写出从左至右前三组的频率;
(2)在图中补画28.5分~30分一组的小矩形;
(3)求测试时抽样的人数;
(4)求测试成绩的中位数落在第几组;
(5)如果全区共有3600名九年级学生,估计成绩大于27分的学生约有多少人?
【答案】(1)0.06,0.15,0.24;(2)详见解析;(3)400;(4)第4组;(5)1980.
【解析】
(1)纵轴表示频率÷组距,那么频率=纵轴上的数×组距;
(2)最后一组的频率=1-0.06-0.15-0.24-0.31=0.24,那么纵轴高为0.24÷1.5=0.16;
(3)这两组的频率之差为:0.31-0.24=0.07,所以样本总数为:28÷0.07=400;
(4)中位数也应在按次序排列后的频率的正中间,前三组的频率之和为:0.06+0.15+0.24=0.45,所以中位数应在第四组;
(5)大于27分的应是后2组,频率之和为:0.24+0.31=0.55,得到成绩大于27分的学生数为3600×0.55.
(1)从左至右前三组的频率分别为![]() ,
,![]() ,
,![]() .(2)28.5分~30分小组间的频率为
.(2)28.5分~30分小组间的频率为![]()
则小长方形的高为0.16.
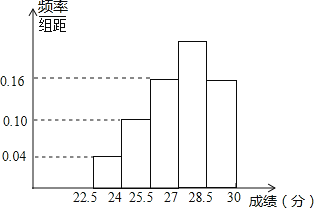
(3)测试时抽样的人数为示![]() (人);
(人);
(4)测试成绩的中位数落在第四组,因为22.5分~24分的有24人,24分~25.5分的有60人,25.5分~27分的有96人,27分~28.5分的有124人,28.5分~30分的有96人,则其中位数落在第四组.
(5)3600人中成绩大于27分的学生有![]() (人),
(人),


科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.若小文早餐吃了两个粽子,求这两个粽子刚好都是花生馅粽的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例图数y=![]() (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y=
(x<0)图象上一点,AC⊥x轴于点C,与反比例函数y=![]() (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
(x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
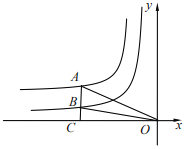
A.﹣4B.﹣6C.﹣8D.﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
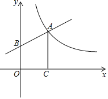
【题目】如图,已知点A在反比例函数![]() (x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(1)求点A的坐标;
(2)若四边形ABOC的面积是![]() ,求一次函数y=kx+b的表达式.
,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com