

分析 (1)利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系,再把∠A代入即可求∠BOC的度数.
(2)先根据外角平分线的性质求出∠B′C′O′、∠O′B′C′与∠A′的关系,再由三角形内角和定理解答即可;
(3)根据(1)(2)中所得的∠BOC和∠B′O′C′与∠A和∠A′的关系可得答案.
解答 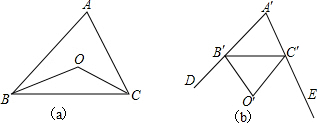 解:(1)∵BO、CO分别平分∠ABC和∠ACB,
解:(1)∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-($\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A.
当∠A=40°时,
∠BOC=90°+$\frac{1}{2}$∠A=110°.
(2)∵B′O′、C′O′是△ABC的两个外角的平分线,
∴∠B′C′O′=$\frac{1}{2}$(∠A′+∠A′B′C′),∠O′B′C′=$\frac{1}{2}$(∠A′+∠A′C′B′),
∵∠B′C′A′+∠A′B′C′=180°-∠A′,
∴∠B′O′C′=180°-∠O′B′C′-∠O′C′B′,
=180°-$\frac{1}{2}$(∠A′+∠A′B′C′+∠A′+∠A′C′B′),
=180°-$\frac{1}{2}$(180°+∠A′),
=90°-$\frac{1}{2}$∠A′.
∵∠A′=40°,
∴∠B′O′C′=90°-20°=70°;
(3)∠BOC-∠B′O′C′=∠A=40°,
∠BOC-∠B′O′C′=∠A=n°,
∵∠BOC=90°+$\frac{1}{2}$∠A,∠B′O′C′=90°-$\frac{1}{2}$∠A′,
∴∠BOC-∠B′O′C′=∠A=n°.
点评 本题考查的是三角形内角和定理,以及三角形内角与外角的关系,熟知三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
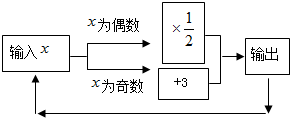 如图所示的运算程序中,
如图所示的运算程序中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
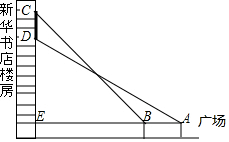 如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6m到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21m,则该屏幕上端与下端之间的距离CD为(21-9$\sqrt{3}$)m.
如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6m到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21m,则该屏幕上端与下端之间的距离CD为(21-9$\sqrt{3}$)m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题:求解关于x的一元二次不等式a(x-x1)(x-x2)>0(a≠0,x1<x2)
问题:求解关于x的一元二次不等式a(x-x1)(x-x2)>0(a≠0,x1<x2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com