
如图,已知反比例函数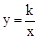 与一次函数
与一次函数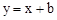 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1,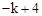 ),
),
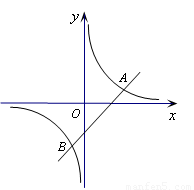
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
(1)反比例函数的表达式为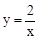 ,一次函数的表达式为y=x+1;(2)x<-2或0<x<1.
,一次函数的表达式为y=x+1;(2)x<-2或0<x<1.
【解析】
试题分析:(1)把A(1,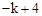 )代入解析式
)代入解析式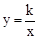 ,即可求出k的值;把求出的A点坐标代入一次函数y=x+b的解析式,即可求出b的值;从而求出这两个函数的表达式;
,即可求出k的值;把求出的A点坐标代入一次函数y=x+b的解析式,即可求出b的值;从而求出这两个函数的表达式;
(2)将两个函数的解析式组成方程组,其解即为另一点的坐标.当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出一次函数的值小于反比例函数的值x的取值范围.
试题解析:(1)∵已知反比例函数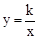 经过点A(1,
经过点A(1,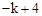 ),
),
∴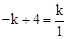 ,解得∴k=2. ∴A(1,2).
,解得∴k=2. ∴A(1,2).
∵一次函数y=x+b的图象经过点A(1,2),∴2=1+b,解得b=1.
∴反比例函数的表达式为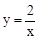 ,一次函数的表达式为y=x+1.
,一次函数的表达式为y=x+1.
(2)由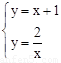 消去y,得
消去y,得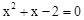 ,即
,即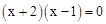 ,∴x=-2或x=1.∴y=-1或y=2.
,∴x=-2或x=1.∴y=-1或y=2.
∴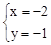 或
或
∵点B在第三象限,∴点B的坐标为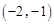 .
.
由图象可知,当反比例函数的值大于一次函数的值时,x的取值范围是x<-2或0<x<1.
考点:1.反比例函数与一次函数的交点问题;2.曲线上点的坐标与方程的关系;3.解一元二次方程.


科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| m |
| x |
| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y1=
如图,已知反比例函数y1=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com