

分析 问题解决:(1)只要找准了图形的间的底边和底边之间的关系,高和高之间的关系,再根据面积公式来计算就不难理解其中的规律了;
(2)只要找准了图形的间的底边和底边之间的关系,高和高之间的关系,三角形的三条中线的交点分每条中线成1:2关系,再根据面积公式来计算就不难理解其中的规律了;
问题拓广:
(1)借助问题再现的结论S△BCD=$\frac{1}{2}$S△ABC即可,
(2)借助问题解决(1)中的结论S△BOD=S△COE即可;
(3)借助问题解决(1)中的结论S△BOD=S△COE即可;
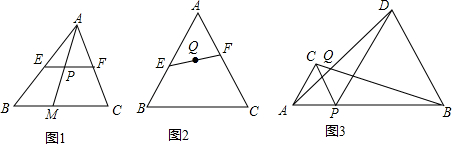
解答 解:问题2::S△BOD=S△COE成立,
理由:∵△ABC中,CD为AB边上的中线,
∴S△BCD=$\frac{1}{2}$S△ABC,
∵BE为AC边上的中线,
∴S△CBE=$\frac{1}{2}$S△ABC
∴S△BCD=S△CBE
∵S△BCD=S△BOD+S△BOC,S△CBE=S△COE+S△BOC
∴S△BOD=S△COE
(2)由(1)有S△BOD=S△COE,
同(1)方法得,S△BOD=S△AOD,
S△COE=S△AOE,
S△BOF=S△COF,
∴S△BOD=S△COE=S△AOE=S△AOD,
∵点O是三角形三条中线的交点,
∴OA=2OF,
∴S△AOC=2S△COF=S△AOE+S△COE=2S△COE,
∴S△COF=S△COE,
∴S△BOD=S△COE=S△AOE=S△AOD=S△BOF=S△COF,
∴S△BOD=$\frac{1}{6}$S△ABC,
故答案为$\frac{1}{6}$
问题拓广:
(1)如图4:
连接BD,由问题再现:
S△BDE=$\frac{1}{2}$S△ABD,
S△BDF=$\frac{1}{2}$S△BCD,
∴S阴影=$\frac{1}{2}$S四边形ABCD,
故答案为 $\frac{1}{2}$,
(2)如图5:
连接BD,由问题解决:
S△BMD=$\frac{1}{3}$S△ABD,S△BDN=$\frac{1}{3}$S△BCD,
∴S阴影=$\frac{1}{3}$S四边形ABCD,
故答案为$\frac{1}{3}$;
(3)如图6,
连接AC,BD
由上面的结论得
∵G是四边形ABCD的边AB的中点,
∴S△AGC=$\frac{1}{2}$S△ABC,S△BGC=$\frac{1}{2}$S△ABC
∵H是四边形ABCD的边CD的中点
∴S△AHC=$\frac{1}{2}$S△ACD,S△AHD=$\frac{1}{2}$S△ACD
∴S四边形AGCH=$\frac{1}{2}$S四边形ABCD
同样的方法得到S四边形BFDE=$\frac{1}{2}$S四边形ABCD
∴S四边形AGCH=S四边形BFDE
∴S四边形AGCH=S△ABE+S△DFC
∴S阴=S1+S2+S3+S4=1+1.5+2+2.5=7.
故答案为7.
点评 此题是面积与等积变形问题,集中考查了三角形的面积公式,解本题的关键是面积之间的转化.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
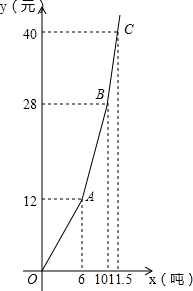 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).| 每月水用量 | 单价 |
| 不超出6吨的部分 | 2元/吨 |
| 超出6吨不超出10吨的部分 | 4 元/吨 |
| 超出10吨的部分 | 8元/吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4+9}=\sqrt{4}+\sqrt{9}$ | B. | 2$\sqrt{2}-\sqrt{2}$=2 | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\frac{{\sqrt{21}}}{{\sqrt{3}}}=\sqrt{\frac{21}{3}}=\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有理数都是有限小数 | |
| B. | 同旁内角互补 | |
| C. | 函数y=$\frac{1}{\sqrt{x-3}}$自变量x的取值范围是x≥3 | |
| D. | 若甲、乙两组数据中各有20个数据,平均数$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,方差S甲2=1.25,S乙2=0.96,则说明乙组数据比甲组数据稳定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com