
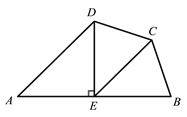
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的垂直平分线,连接
边的垂直平分线,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
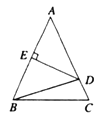
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于点D、E,若△ABC和△BDC 的周长分别为40cm和25cm ,则BC=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]()
(1)蜗牛最后是否回到出发点?请说明理由;
(2)蜗牛离开出发点![]() 最远时是_______厘米;
最远时是_______厘米;
(3)在爬行过程中,如果蜗牛每爬2厘米奖励一粒芝麻,求蜗牛-共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
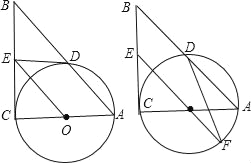
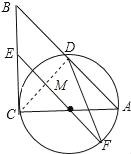
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,
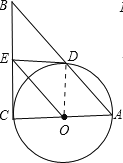
∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()
【题型】解答题
【结束】
23
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边上的高,连接
边上的高,连接![]() ,过点
,过点![]() 作
作![]() 与点
与点![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]() .
.
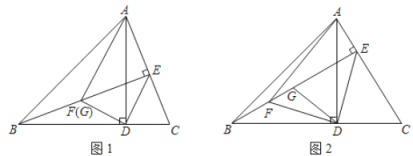
(1)如图![]() ,若点
,若点![]() 与点
与点![]() 重合,求证:
重合,求证:![]() ;
;
(2)如图![]() ,请写出
,请写出![]() 与
与![]() 之间的关系并证明.
之间的关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,小彬从该网店购买了3筒甲种羽毛球和2筒乙种羽毛球,一共花费270元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定购进甲、乙两种羽毛球各80筒.已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.元旦期间该网店开展优惠促销活动,甲种羽毛球打折销售,乙种羽毛球售价不变,若所购进羽毛球均可全部售出,要使全部售出所购进的羽毛球的利润率是![]() ,那么甲种羽毛球是按原销售价打几折销售的.
,那么甲种羽毛球是按原销售价打几折销售的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某品牌的羽毛球拍和乒乓球拍,羽毛球拍每副定价![]() 元,乒乓球拍每副定价
元,乒乓球拍每副定价![]() 元.店庆期间该超市开展促销活动,活动期间向顾客提供两种优惠方案.
元.店庆期间该超市开展促销活动,活动期间向顾客提供两种优惠方案.
方案一:买一副羽毛球拍送一副乒乓球拍;
方案二:羽毛球拍和乒乓球拍都按定价的![]() 付款.
付款.
现某校要到该超市购买羽毛球拍![]() 副,乒乓球拍
副,乒乓球拍![]() 副(
副(![]() )
)
(1)若该校按方案一购买,需付款____元;(用含![]() 的代数式表示),若该校按方案二购买,需付款_____元.(用含
的代数式表示),若该校按方案二购买,需付款_____元.(用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 取何值时,两种方案一样优惠?
取何值时,两种方案一样优惠?
(3)当![]() 时,通过计算说明此时按哪种方案购买较为合算?你能给出一种更为省钱的购买方法吗?请写出你的购买方法,并计算需付款多少元?
时,通过计算说明此时按哪种方案购买较为合算?你能给出一种更为省钱的购买方法吗?请写出你的购买方法,并计算需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
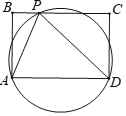
【题目】在矩形ABCD中,AB=4,BC=6,动点P为矩形边上的一点,点P沿着B﹣C的路径运动(含点B和点C),则△ADP的外接圆的圆心O的运动路径长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com