
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BO于H.连接OG、CG.
(1)求证:AH=BE;
(2)试探究:∠AGO 的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.

【答案】(1)见解析;(2)45°;(3)9.
【解析】
(1)利用正方形性质,证△ABH≌△BCE.可得AH=BE.
(2)证△AOH∽△BGH,![]() ,
,![]() ,再证△OHG∽△AHB.,
,再证△OHG∽△AHB.,
得∠AGO=∠ABO=45°;
(3)先证△ABG∽△BFG.得![]() ,所以,AG·GF=BG2
,所以,AG·GF=BG2
=(![]() )2=18.再证△AGO∽△CGF.得
)2=18.再证△AGO∽△CGF.得![]() ,所以,GO·CG=AG·GF=18.所以,S△OGC=
,所以,GO·CG=AG·GF=18.所以,S△OGC=![]() CG·GO.
CG·GO.
解:(1)∵四边形ABCD是正方形,
∴∠ABC=90°,AB=CB,∠ABO=∠ECB=45°
∵AF⊥BE,
∴∠BAG+∠ABG=∠CBE+∠ABG=90°.
∴∠BAH=∠CBE.
∴△ABH≌△BCE.
∴AH=BE.
(2)∵∠AOH=∠BGH=90°,∠AHO=∠BHG,
∴△AOH∽△BGH
∴![]()
∴![]()
∵∠OHG=∠AHB.
∴△OHG∽△AHB.
∴∠AGO=∠ABO=45°,即∠AGO的度数为定值
(3)∵∠ABC=90°,AF⊥BE,
∴∠BAG=∠FBG,∠AGB=∠BGF=90°,
∴△ABG∽△BFG.
∴![]() ,
,
∴AG·GF=BG2=(![]() )2=18.
)2=18.
∵△AHB∽△OHG,
∴∠BAH=∠GOH=∠GBF.
∵∠AOB=∠BGF=90°,
∴∠AOG=∠GFC.
∵∠AGO=45°,CG⊥GO,
∴∠AGO=∠FGC=45°.
∴△AGO∽△CGF.
∴![]() ,
,
∴GO·CG=AG·GF=18.
∴S△OGC=


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为 . (精确到1m)
【参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7】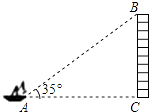
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)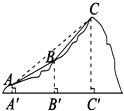
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,若AB=6,BC=![]() ,则CF的长为_______
,则CF的长为_______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.
(1)如图①,求证直线DE是⊙O的切线; 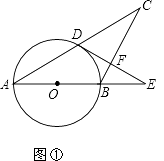
(2)如图②,作DG⊥AB于H,交⊙O于G,若AB=5,AC=8,求DG的长. 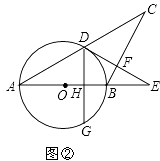
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,E,F分别是AB,AD的中点,DE,BF相交于点G,连接BD,CG,有下列结论:①∠BGD=120° ;②BG+DG=CG;③△BDF≌△CGB;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com