
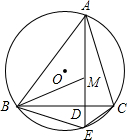
 如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.
如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.分析 (1)由圆周角定理可知:∠BAE=∠BCE,所有易证△ABD∽△CED,利用对应边的比相等即可求出CD的长度;
(2)因为M是△ABC的内心,所以AE、BM分别平分∠BAC、∠ABC,所以∠BAE=∠EBC,∠ABM=∠CNM,所以∠EBM=∠EMB;
(3)任意一个三角形都能确定一个圆,且该圆的圆心是三角形任意两边的垂直平分线的交点,由(2)证明过程可知OE是BC的垂直平分线,BM的垂直平分线过点E,所以圆心是点E,半径为BE.
解答  解:(1)∵$\widehat{BE}=\widehat{BE}$,
解:(1)∵$\widehat{BE}=\widehat{BE}$,
∴∠BAE=∠BCE,
∵∠ADB=∠CDE,
∴△ABD∽△CED,
∴$\frac{AB}{CE}=\frac{AD}{CD}$,
∵AB=2CE,AD=6,
∴$\frac{2CE}{CE}=\frac{6}{CD}$,
∴CD=3;
(2)∵M是△ABC的内心,
∴AE平分∠BAC,
∴∠BAE=∠CAE,
∴$\widehat{BE}=\widehat{CE}$,
∴∠BAE=∠EBC,
∵BM平分∠ABC,
∴∠ABM=∠CBM,
∴∠EBC+∠CBM=∠BAE+∠ABM,
∴∠EBM=∠EMB;
(3)B、C、M三个点可以确定一个圆.
该圆的圆心是BC、BM的垂直平分线的交点,
连接OE,
∴由(2)可知:$\widehat{BE}=\widehat{CE}$,
由垂径定理可知:OE垂直平分线段BC,
又由(2)可知:∠EBM=∠EMB,
∴△BEM是等腰三角形,
∴由三线合一可知:线段BM的垂直平分线必过点E,
∴它们确定的圆的圆心为点E,半径为BE(或ME、EC)的长度.
点评 本题考查三角形外心与内心的性质,涉及圆周角定理,垂径定理,相似三角形的性质与判定,等腰三角形的性质等知识,考查学生灵活运用知识的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | x≤2 | B. | x<4 | C. | 2≤x<4 | D. | x≥2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3<x≤5 | B. | 3<x≤5 | C. | 3<x≤-5 | D. | -3<x<5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
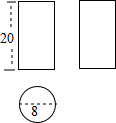 如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )| A. | 128πcm2 | B. | 160πcm2 | C. | 176πcm2 | D. | 192πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
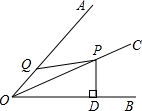
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
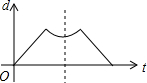 设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )
设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )| A. |  | B. | 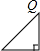 | C. | 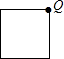 | D. | 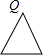 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com