
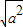 =|a|变形后,再利用完全平方公式化简,将表示出的x1+x2及x1x2代入,化简后根据m大于6,可得出AB的长大于1,故③正确;利用顶点坐标公式表示出抛物线的顶点坐标,代入y=-2(x-1)2中经验,可得出抛物线的顶点在y=-2(x-1)2图象上,故④正确,综上,得到正确的序号.
=|a|变形后,再利用完全平方公式化简,将表示出的x1+x2及x1x2代入,化简后根据m大于6,可得出AB的长大于1,故③正确;利用顶点坐标公式表示出抛物线的顶点坐标,代入y=-2(x-1)2中经验,可得出抛物线的顶点在y=-2(x-1)2图象上,故④正确,综上,得到正确的序号.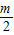 ,x1x2=
,x1x2=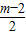 ,
,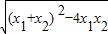 =
=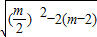 =|
=|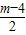 |,
|,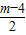 >1,
>1,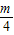 ,
,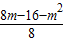 ),
),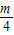 代入得:y=-2(
代入得:y=-2(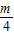 -1)2=-2(
-1)2=-2(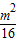 -
-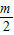 +1)=
+1)=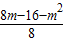 ,
,

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
A、抛物线y=-2x2+3x+1的对称轴是直线x=
| ||
| B、抛物线y=x2-2x-3,点A(3,0)不在它的图象上 | ||
| C、二次函数y=(x+2)2-2的顶点坐标是(-2,-2) | ||
| D、函数y=2x2+4x-3的图象的最低点在(-1,-5) |
查看答案和解析>>
科目:初中数学 来源:第26章《二次函数》中考题集(03):26.1 二次函数(解析版) 题型:选择题
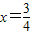
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com