
 ,点B的坐标为(7,4).
,点B的坐标为(7,4).
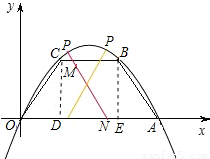 解:(1)过C作CD⊥OA于D,过B作BE⊥OA于E,
解:(1)过C作CD⊥OA于D,过B作BE⊥OA于E, ,
,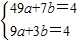 ,
, ,
,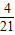 x2+
x2+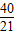 x.
x. (BC+OA)•CD=28.
(BC+OA)•CD=28. S梯形ABCO=14
S梯形ABCO=14
 ,4),N(
,4),N(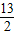 ,0)
,0) x+
x+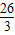 ,联立抛物线的解析式有:
,联立抛物线的解析式有: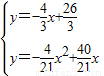 ,
,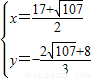 (不合题意舍去),
(不合题意舍去),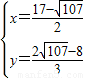 .
.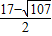 ,
,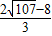 ).
).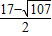 ,
,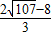 ),(
),(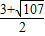 ,
,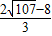 ).
).

 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 ,点B的坐标为(7,4).
,点B的坐标为(7,4).
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《概率》(06)(解析版) 题型:解答题

 ,那么应添加多少张“太阳”卡片?请说明理由.
,那么应添加多少张“太阳”卡片?请说明理由.查看答案和解析>>
科目:初中数学 来源:2010年四川省自贡市仙市中学中考数学一模试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2009年四川省宜宾市中考数学试卷(解析版) 题型:解答题

 ,那么应添加多少张“太阳”卡片?请说明理由.
,那么应添加多少张“太阳”卡片?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com