
 如图,水平地面上竖立着一盏明亮的路灯A,AB垂直地面BC于B.旁边有6级台阶.每级台阶高0.2米,宽0.4米,现有身高1.4米的小明垂直站立在离第一级台阶1.2米的C处时.小明的影子刚好落在第一级台阶的边缘E处.身高0.9米的小华垂直站立在第四级台阶的边缘F处.其影子刚好落在第六级台阶的边缘H处.求路灯AB的高.
如图,水平地面上竖立着一盏明亮的路灯A,AB垂直地面BC于B.旁边有6级台阶.每级台阶高0.2米,宽0.4米,现有身高1.4米的小明垂直站立在离第一级台阶1.2米的C处时.小明的影子刚好落在第一级台阶的边缘E处.身高0.9米的小华垂直站立在第四级台阶的边缘F处.其影子刚好落在第六级台阶的边缘H处.求路灯AB的高. 分析 根据题意得出:△DEI∽△AEN,△AHM∽△GHY,进而利用相似三角形的性质得出AN的长,求出即可.
解答  解:如图所示:过点E作EN⊥AB,垂足为N,交DC于点I,
解:如图所示:过点E作EN⊥AB,垂足为N,交DC于点I,
过点H作HM⊥AB于点M,交FG于点Y,
可得:△DEI∽△AEN,△AHM∽△GHY,
由题意可得:IE=1.2m,DI=1.2m,HY=0.8m,GY=0.5m,BM=1.2m,MN=1m,
则$\frac{DI}{EI}$=$\frac{AN}{NE}$,$\frac{GY}{HY}$=$\frac{AM}{MH}$,
故$\frac{1.2}{1.2}$=$\frac{AN}{NE}$,$\frac{0.5}{0.8}$=$\frac{AN-MN}{AN-1.2+3.2}$,
解得:AN=6,
故AB=AN+BN=6+0.2=6.2(m).
答:路灯AB的高为6.2m.
点评 此题主要考查了相似三角形的应用,根据题意得出对应线段长是解题关键.


科目:初中数学 来源: 题型:解答题
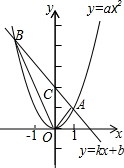 已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.
已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
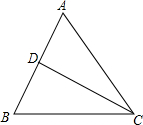 如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论:
如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
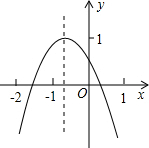 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com