
分析 根据题意画出图形,分为两种情况,求出OM长,根据旋转的性质得出OM=OF=OE,即可求出答案.
解答 解:分为两种情况:①当绕着坐标原点O顺时针旋转60°后到E点时,连接MN,过M作MA⊥x轴于A,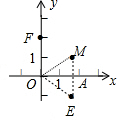
∵根据旋转的性质得出OM=OE,∠MOE=60°,
∴△MOE是等边三角形,
∵M($\sqrt{3}$,1),
∴tanA=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠MOA=30°,OM=2MA=2,
∴∠EOA=60°-30°=30°,
∵OM=OE,
∴x轴垂直平分MN,
∵M($\sqrt{3}$,1),
∴E($\sqrt{3}$,-1),
②当绕着坐标原点O逆时针旋转60°后到F点时,∠MOF=60°,OF=OM=2,
∵∠MOA=30°,
∴∠FOA=90°,
即F点在y轴上,如图,此时F的坐标为(0,2),
故答案为:$(\sqrt{3},-1)$或(0,2).
点评 本题考查了旋转的性质,图形与坐标特点等知识点,能求出符合的所有情况是解此题的关键.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
 已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.
已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
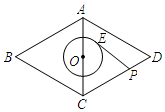 如图,已知菱形ABCD的边长为4,∠B=60°,点O为对角线AC的中点,⊙O
如图,已知菱形ABCD的边长为4,∠B=60°,点O为对角线AC的中点,⊙O查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC、BC分别交于点D、E,连接AE,当AB=3,AC=5时,△ABE的周长等于( )
如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC、BC分别交于点D、E,连接AE,当AB=3,AC=5时,△ABE的周长等于( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 班级 | 参加人数 | 中位数 | 方差 | 平均数 |
| (1)班 | 50 | 120 | 103 | 122 |
| (2)班 | 49 | 121 | 201 | 122 |
| A. | 两班平均成绩一样 | B. | (1)班的优秀人数多于(2)班 | ||
| C. | (2)班的两极分化比(1)班严重 | D. | (1)班的总体成绩稳定一些 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
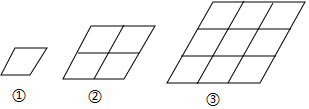
| A. | 50 | B. | 80 | C. | 91 | D. | 140 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com